روش حداقل مربعات روشی در تحلیل رگرسیون است که برای حل دستگاه معادلاتی به کار می رود که تعداد معادله هایش بیش از تعداد مجهول هایش است. مهم ترین کاربرد روش کمترین مربعات در برازش منحنی بر داده ها است. مدل برازش شده بر داده ها، مدلی است که در آن کمیت χ 2 کمینه باشد.
χ 2 = ∑ i = 1 N ( y i − f ( x i → , β → ) ) 2 σ y , i 2
این روش را نخستین بار کارل فردریش گاوس در سال ۱۷۹۴ استفاده کرد. [ ۱] روش حداقل مربعات در زبان برنامهٔ نویسی R، بیشتر نرم افزارهای آماری و ریاضی ( مانند Excel, SPSS, MATLAB و … ) و ماشین حساب های مهندسی وجود دارد.
منشأ روش حداقل مربعات از نجوم و یافتن موقعیت ستارگان بوده است.
برای برازش منحنی y = f ( x → ) بر داده ها، فرض می کنیم اندازه گیری ها مستقل از هم انجام شده اند و خطای x → نیز در مقابل خطای y قابل صرف نظر است ( مقادیر x → بدون خطا هستند ) . تابع f علاوه بر x → ، به ثوابتی که آن ها را با بردار β → نشان می دهیم بستگی دارند. هدف، پیدا کردن مقادیر β → است، به گونه ای که تابع f ( x → , β → ) دقیق ترین پیش بینی را از y ارائه دهد. به این منظور، کمیت باقی مانده را به صورت
d i = y i − f ( x → i , β → )
تعریف می کنیم. اگر هر y i از توزیع نرمال حول مقدار واقعی f ( x → i , β → ) با پهنای σ y , i پیروی کند، احتمال به دست آوردن y i متناسب است با:
P r o b β → ( y i ) ∝ 1 σ y , i 2 e − d i 2 / 2 / σ y , i 2
است. احتمال مشاهدهٔ تمام مقادیر y این طور به دست می آید:
P r o b β → ( y 1 , y 2 , . . . , y N ) = P r o b β → ( y 1 ) × P r o b β → ( y 2 ) × . . . × P r o b β → ( y N )
∝ 1 ∏ i = 1 N σ y , i e − χ 2 / 2
کمیت χ 2 که در نما قرار دارد به صورت
χ 2 = ∑ i = 1 N ( y i − f ( x i → , β → ) ) 2 σ y , i 2 = ∑ i = 1 N d i 2 σ y , i 2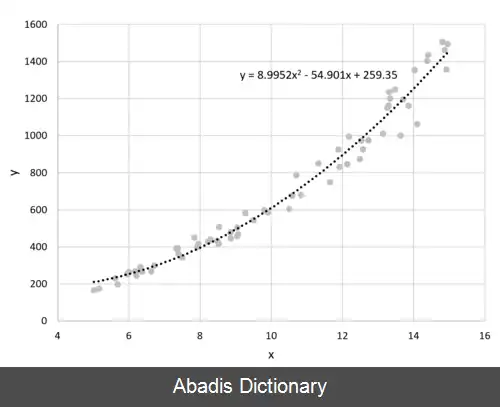
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفχ 2 = ∑ i = 1 N ( y i − f ( x i → , β → ) ) 2 σ y , i 2
این روش را نخستین بار کارل فردریش گاوس در سال ۱۷۹۴ استفاده کرد. [ ۱] روش حداقل مربعات در زبان برنامهٔ نویسی R، بیشتر نرم افزارهای آماری و ریاضی ( مانند Excel, SPSS, MATLAB و … ) و ماشین حساب های مهندسی وجود دارد.
منشأ روش حداقل مربعات از نجوم و یافتن موقعیت ستارگان بوده است.
برای برازش منحنی y = f ( x → ) بر داده ها، فرض می کنیم اندازه گیری ها مستقل از هم انجام شده اند و خطای x → نیز در مقابل خطای y قابل صرف نظر است ( مقادیر x → بدون خطا هستند ) . تابع f علاوه بر x → ، به ثوابتی که آن ها را با بردار β → نشان می دهیم بستگی دارند. هدف، پیدا کردن مقادیر β → است، به گونه ای که تابع f ( x → , β → ) دقیق ترین پیش بینی را از y ارائه دهد. به این منظور، کمیت باقی مانده را به صورت
d i = y i − f ( x → i , β → )
تعریف می کنیم. اگر هر y i از توزیع نرمال حول مقدار واقعی f ( x → i , β → ) با پهنای σ y , i پیروی کند، احتمال به دست آوردن y i متناسب است با:
P r o b β → ( y i ) ∝ 1 σ y , i 2 e − d i 2 / 2 / σ y , i 2
است. احتمال مشاهدهٔ تمام مقادیر y این طور به دست می آید:
P r o b β → ( y 1 , y 2 , . . . , y N ) = P r o b β → ( y 1 ) × P r o b β → ( y 2 ) × . . . × P r o b β → ( y N )
∝ 1 ∏ i = 1 N σ y , i e − χ 2 / 2
کمیت χ 2 که در نما قرار دارد به صورت
χ 2 = ∑ i = 1 N ( y i − f ( x i → , β → ) ) 2 σ y , i 2 = ∑ i = 1 N d i 2 σ y , i 2

wiki: کمترین مربعات
