در هندسهٔ تحلیلی زاویه های هادی یک بردار اعدادی برابر زوایای بین آن بردار و محور های مختصات هستند. [ ۱]
کسینوس های هادی آن بردار نیز برابر کسینوس زوایای هادی آن هستند.
در مواردی نیز این اصطلاح برای زاویهٔ بین دو بردار تعریف می شود. [ ۲]
اگر زاویهٔ بین بردار a → = ( a 1 , a 2 , a 3 ) و محور های x و y و z به ترتیب برابر α و β و γ باشد ( 0 ⩽ α , β , γ ⩽ π ) ، کسینوس های هادی به صورت زیر محاسبه می شوند[ ۱] :
cos α = a 1 | a → | cos β = a 2 | a → | cos γ = a 3 | a → |
که با جایگذاری | a → | = a 1 2 + a 2 2 + a 3 2 و جمع مجذور این مقادیر به تساوی زیر می رسیم[ ۱] :
cos 2 α + cos 2 β + cos 2 γ = 1
این تساوی را می توان به ابعاد بیشتر نیز تعمیم داد.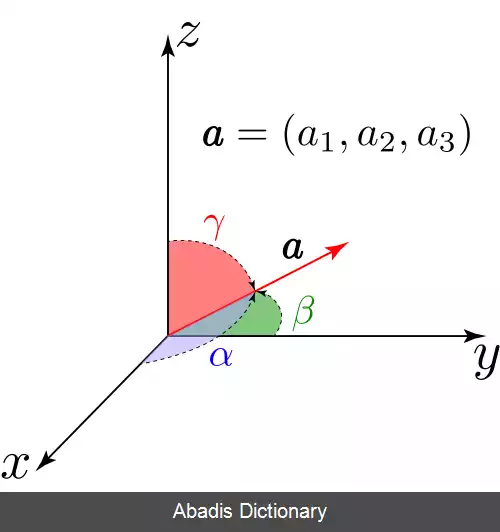
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفکسینوس های هادی آن بردار نیز برابر کسینوس زوایای هادی آن هستند.
در مواردی نیز این اصطلاح برای زاویهٔ بین دو بردار تعریف می شود. [ ۲]
اگر زاویهٔ بین بردار a → = ( a 1 , a 2 , a 3 ) و محور های x و y و z به ترتیب برابر α و β و γ باشد ( 0 ⩽ α , β , γ ⩽ π ) ، کسینوس های هادی به صورت زیر محاسبه می شوند[ ۱] :
cos α = a 1 | a → | cos β = a 2 | a → | cos γ = a 3 | a → |
که با جایگذاری | a → | = a 1 2 + a 2 2 + a 3 2 و جمع مجذور این مقادیر به تساوی زیر می رسیم[ ۱] :
cos 2 α + cos 2 β + cos 2 γ = 1
این تساوی را می توان به ابعاد بیشتر نیز تعمیم داد.

wiki: کسینوس هادی
