در هندسه، از کره های دندلین ( انگلیسی: Dandelin spheres ) برای اثبات بیضی بودن تقاطع یک صفحه و یک مخروط در صورت ناموازی بودن صفحه با قاعده، ارتفاع و یال آن استفاده می شود.
در ۱۸۲۲ ریاضی دان بلژیکی جرمینال پیر دندلین با ابداع کره های دندلین اثبات کرد که بیضی ساخته شده با استفاده از تعریف کانونی و بیضی ساخته شده با برخورد صفحه و مخروط یکی اند. [ ۱] در ۱۸۲۹ نیز پیرس مورتون[ الف] با استفاده از کره های دندلین ثابت کرد که بیضی ساخته شده با تعریف کانون و خط هادی هم با بیضی ساخته شده در تقاطع صفحه و مخروط یکی است. [ نیازمند منبع]
با استفاده از کره های دندلین می توان اثبات کرد که بیضی تعریف شده با دو کانون با بیضی ساخته شده از برخورد مخروط و صفحه یکی است. [ ۲] گیریم صفحهٔ e مخروطی را قطع می کند و در محل انقطاع یک منحنی تشکیل شده است. دو کرهٔ دندلین G 1 روی صفحه و G 2 زیر صفحه تعریف شده اند. تقاطع هر کره با مخروط یک دایره است ( k 1 و k 2 ) ، و هر کره بر صفحهٔ e را در یک نقطه ( F 1 و F 2 ) مماس است. گیریم P نقطه ای روی منحنی باشد. قصد است که ثابت شود با حرکت P بر روی منحنی، فاصلهٔ d ( F 1 , P ) + d ( F 2 , P ) ثابت می ماند:
• گیریم خطی که از P {\displaystyle P} و رأس S {\displaystyle S} می گذرد دو دایره را در نقاط P 1 {\displaystyle P_{1}} و P 2 {\displaystyle P_{2}} قطع کند.
• با حرکت P {\displaystyle P} بر روی منحنی، P 1 {\displaystyle P_{1}} و P 2 {\displaystyle P_{2}} بر روی دو دایره حرکت می کنند.
• P F 1 {\displaystyle PF_{1}} و P P 1 {\displaystyle PP_{1}} هر دو از نقطهٔ P {\displaystyle P} آغاز شده اند و بر دایرهٔ G 1 {\displaystyle G_{1}} مماسند، پس P F 1 = P P 1 {\displaystyle PF_{1}=PP_{1}} ( چرا که دو مثلث قائم الزاویهٔ M P F 1 {\displaystyle MPF_{1}} و M P P 1 {\displaystyle MPP_{1}} همنهشتند ) .
• به همین ترتیب P F 2 = P P 2 {\displaystyle PF_{2}=PP_{2}} .
• از آنجا که k 1 {\displaystyle k_{1}} و k 2 {\displaystyle k_{2}} موازی اند، فاصلهٔ P 1 {\displaystyle P_{1}} و P 2 {\displaystyle P_{2}} همواره عدد ثابتی است؛ بنابراین با حرکت P {\displaystyle P} روی منحنی فاصلهٔ d ( F 1 , P ) + d ( F 2 , P ) {\displaystyle d ( F1, P ) +d ( F2, P ) } ثابت می ماند. پس ثابت می شود که منحنی مورد بحث همان بیضی است. [ ۳]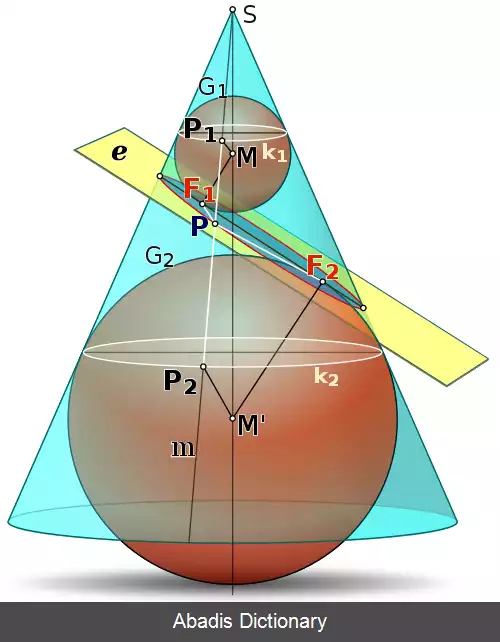

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر ۱۸۲۲ ریاضی دان بلژیکی جرمینال پیر دندلین با ابداع کره های دندلین اثبات کرد که بیضی ساخته شده با استفاده از تعریف کانونی و بیضی ساخته شده با برخورد صفحه و مخروط یکی اند. [ ۱] در ۱۸۲۹ نیز پیرس مورتون[ الف] با استفاده از کره های دندلین ثابت کرد که بیضی ساخته شده با تعریف کانون و خط هادی هم با بیضی ساخته شده در تقاطع صفحه و مخروط یکی است. [ نیازمند منبع]
با استفاده از کره های دندلین می توان اثبات کرد که بیضی تعریف شده با دو کانون با بیضی ساخته شده از برخورد مخروط و صفحه یکی است. [ ۲] گیریم صفحهٔ e مخروطی را قطع می کند و در محل انقطاع یک منحنی تشکیل شده است. دو کرهٔ دندلین G 1 روی صفحه و G 2 زیر صفحه تعریف شده اند. تقاطع هر کره با مخروط یک دایره است ( k 1 و k 2 ) ، و هر کره بر صفحهٔ e را در یک نقطه ( F 1 و F 2 ) مماس است. گیریم P نقطه ای روی منحنی باشد. قصد است که ثابت شود با حرکت P بر روی منحنی، فاصلهٔ d ( F 1 , P ) + d ( F 2 , P ) ثابت می ماند:
• گیریم خطی که از P {\displaystyle P} و رأس S {\displaystyle S} می گذرد دو دایره را در نقاط P 1 {\displaystyle P_{1}} و P 2 {\displaystyle P_{2}} قطع کند.
• با حرکت P {\displaystyle P} بر روی منحنی، P 1 {\displaystyle P_{1}} و P 2 {\displaystyle P_{2}} بر روی دو دایره حرکت می کنند.
• P F 1 {\displaystyle PF_{1}} و P P 1 {\displaystyle PP_{1}} هر دو از نقطهٔ P {\displaystyle P} آغاز شده اند و بر دایرهٔ G 1 {\displaystyle G_{1}} مماسند، پس P F 1 = P P 1 {\displaystyle PF_{1}=PP_{1}} ( چرا که دو مثلث قائم الزاویهٔ M P F 1 {\displaystyle MPF_{1}} و M P P 1 {\displaystyle MPP_{1}} همنهشتند ) .
• به همین ترتیب P F 2 = P P 2 {\displaystyle PF_{2}=PP_{2}} .
• از آنجا که k 1 {\displaystyle k_{1}} و k 2 {\displaystyle k_{2}} موازی اند، فاصلهٔ P 1 {\displaystyle P_{1}} و P 2 {\displaystyle P_{2}} همواره عدد ثابتی است؛ بنابراین با حرکت P {\displaystyle P} روی منحنی فاصلهٔ d ( F 1 , P ) + d ( F 2 , P ) {\displaystyle d ( F1, P ) +d ( F2, P ) } ثابت می ماند. پس ثابت می شود که منحنی مورد بحث همان بیضی است. [ ۳]


wiki: کره های دندلین
