در ریاضیات، کره ریمان که به افتخار برنهارت ریمان نامگذاری شده است؛ تنها راه برای نمایش صفحه گسترش یافته مختلط است ( صفحه مختلط به اضافهٔ یک نقطه در بینهایت ) به طوری که دقیقاً نقطه در بی نهایت به مانند یک عدد مختلط دیده می شود. کاربرد اصلی آن در رابطه با توابع مختلط گسترش یافته است ( که می توانند در بینهایت تعریف شوند یا به ازای اعداد مختلطی مقدار بی نهایت بگیرند ) . به همین طریق می توانند در نقطهٔ بی نهایت به مانند هر عدد مختلط دیگر پیوستگی و مشتق پذیری را ملحوظ دارند. از دید هندسی صفحه که با نقاط، خطوط، و زوایا به استثنای فاصله ها سروکار دارد، کره ریمان با اضافه کردن یک نقطه در بی نهایت که تمام خطوط را قطع می کند ساخته می شود که در آن نقطه، خطوط موازی مماس با یکدیگر، و بقیه خطها با همان زاویه ای که در نقطهٔ برخورد موجود دارند یکدیگر را قطع می کنند. این هندسه به عنوان هندسهٔ کرهٔ دو بعدی شناخته می شود که از صفحهٔ گسترش یافتهٔ مختلط با استفاده از کنج نگاری شکل گرفته است. به فرمی که خطها، در صفحهٔ مختلط به دایره هایی از میان بینهایت تبدیل می شوند. زاویه ها در کرهٔ ریمان همان زاویه ها در صفحهٔ مختلط هستند ( و به همان درستی، زوایا در بی نهایت همان زوایا با انتخاب طبیعی بین دو خط می باشند. ) از نظر توپولوژیکی کره ریمان فشرده سازی تک نقطه ای از صفحهٔ مختلط است. کره ریمان را می توان به راحتی با یک کره دو بعدی هندسی تعریف کرد. در نگاه کلی نقطهٔ بی نهایت نقش یکسانی در قبال تمام نقاط واقع در صفحهٔ مختلط دارد.
تعریف می کنیم C ^ = C ∪ { ∞ } ( برای مثال صفحهٔ مختلط گسترش یافته ) . کرهٔ ریمان بر اساس یک تبدیل از C ^ به C ^ در فرم است.
که
ما کرهٔ ریمان را به مثابه یک کره در فضای سه بعدی تصور می کنیم. مثلاً در R 3 . در ارتباط با تبدیل بالا هر نقطه دو مؤلفهٔ z و w است که f ( z ) کره را به خودش تبدیل می کند.
برای برقراری تناظر یک به یک میان نقاط روی صفحهٔ مختلط گسترش یافته و کره ریمان، ما نخست z صفحه را مماس با قطب شمال کره قرار می دهیم. و سپس کنج نکاری را از قطب جنوب کره اعمال می کنیم. به این طریق که از قطب جنوب خطی که صفحهٔ مختلط و کره را قطع می کند را رسم می کنیم. که تناظر یک به یک منحصربه فرد مطلوب را ایجاد می کند. برای کامل کردن این تناظر یک به یک ما پیرو قاعدهٔ بالا قطب جنوب را z = ∞ . قرار می دهیم، با توجه به این که z = 0 قطب شمال است.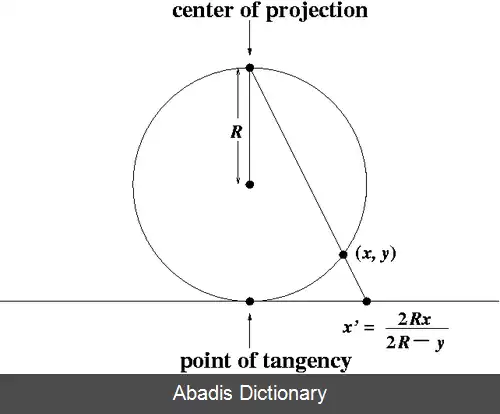
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتعریف می کنیم C ^ = C ∪ { ∞ } ( برای مثال صفحهٔ مختلط گسترش یافته ) . کرهٔ ریمان بر اساس یک تبدیل از C ^ به C ^ در فرم است.
که
ما کرهٔ ریمان را به مثابه یک کره در فضای سه بعدی تصور می کنیم. مثلاً در R 3 . در ارتباط با تبدیل بالا هر نقطه دو مؤلفهٔ z و w است که f ( z ) کره را به خودش تبدیل می کند.
برای برقراری تناظر یک به یک میان نقاط روی صفحهٔ مختلط گسترش یافته و کره ریمان، ما نخست z صفحه را مماس با قطب شمال کره قرار می دهیم. و سپس کنج نکاری را از قطب جنوب کره اعمال می کنیم. به این طریق که از قطب جنوب خطی که صفحهٔ مختلط و کره را قطع می کند را رسم می کنیم. که تناظر یک به یک منحصربه فرد مطلوب را ایجاد می کند. برای کامل کردن این تناظر یک به یک ما پیرو قاعدهٔ بالا قطب جنوب را z = ∞ . قرار می دهیم، با توجه به این که z = 0 قطب شمال است.

wiki: کره ریمان
