کران های چرنوف نام خود را از نام هرمان چرنوف گرفته است که کرانی با کاهش نمایی برای محدود کردن توزیع دنباله ای ( tail distribution ) مجموع تعداد متغیر تصادفی می دهد. این نابربری کرانی بهتر نسبت به نامساوی های دیگر مانند نابرابری مارکف یا نابرابری چبیشف که بر اساس گشتاورهای مرتبه اول و دوم هستند به دست می دهند. اگرچه کران چرنوف لازم دارد که متغیرها مستقل باشند، شرایطی که کران های مارکف و چبیشف لازم نیست.
ارتباط بسیار نزدیکی بین این کران و کران هافدینگ ( Hoeffding's inequality ) و کران برنشتین وجود دارد.
زمانی که تابع مولد گشتاور متغیر تصادفی X معلوم باشد، می توانیم کرانهای خوبی برای {P{X≤a بدست آوریم.
چون کران های چرنوف برای همه tهای مثبت و منفی برقرار است، می توان بهترین کران برای {P{X≥a را با استغاده از مقداری از t که ( e - taM ( t را حداقل می کند به دست آورد. 'کران های چرنوف برای متغیر تصادفی نرمال استاندارد' اگر Z متغیر تصادفی نرمال استاندارد باشد، آنگاه تابع مولد گشتاور آن M ( t ) =et2/2است. پس کران چرنوف برای {P{Z≥a برای هر t> 0 به صورت زیر است:
حال مقدار t مثبتی که e ( t2/2 ) - ta را حداقل می کند، مقداری است که ( t2/2 ) - ta را حداقل می کند، یعنی t=a است؛ بنابراین برای a> 0 داریم:
حال مثالی از کاربرد این کران را نشان می دهیم. فرض کنیم X1, … , Xn متغیرهای تصادفی مستقل با توزیع برنولی باشند، که هر کدام دارای احتمال p > 1/2 باشند، احتمال رخداد همزمان بیش از n/2 متغیر تصادفی { X k = 1 } برابر است با
کران چرنوف نشان می دهد که رابطهٔ بالا دارای کران پایین زیر است:
توجه کنید که برای تعدادی نمونهٔ تصادفی با توزیع برنولی داریم μ = n p با استفاده از نتایج کران چرنوف ( در ادامه ) می توان نشان داد که
باید توجه کرد که با توجه به خواسته های مسئله می توان از فرم های مختلفی از کران چرنوف استفاده کرد.
تصور کنید سکه ای اریب داریم ( یعنی احتمال رو و پشت با هم یکسان نباشند ) . اکنون سؤال این است که چطور می توان سمتی که دارای احتمال بیشتری است را پیدا؟ جواب ساده این است که سکه را بی نهایب بار پرتاب می کنیم و با حساب کردن احتمال هر سمت، آنی که احتمال بیشتری دارد را انتخاب می کنیم؛ ولی در عمل چنین کاری انکانپذیر نیست. چگونه می توان با تعداد پرتاپ های محدود، با احتمالی خوب، حدسی در مورد احتمال سمتی که دارای احتمال رو/پشت بیشتر زد؟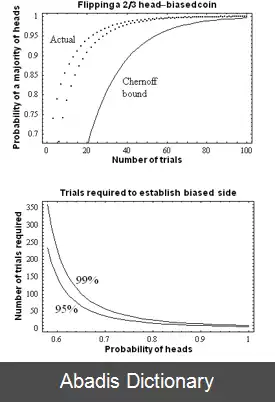
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفارتباط بسیار نزدیکی بین این کران و کران هافدینگ ( Hoeffding's inequality ) و کران برنشتین وجود دارد.
زمانی که تابع مولد گشتاور متغیر تصادفی X معلوم باشد، می توانیم کرانهای خوبی برای {P{X≤a بدست آوریم.
چون کران های چرنوف برای همه tهای مثبت و منفی برقرار است، می توان بهترین کران برای {P{X≥a را با استغاده از مقداری از t که ( e - taM ( t را حداقل می کند به دست آورد. 'کران های چرنوف برای متغیر تصادفی نرمال استاندارد' اگر Z متغیر تصادفی نرمال استاندارد باشد، آنگاه تابع مولد گشتاور آن M ( t ) =et2/2است. پس کران چرنوف برای {P{Z≥a برای هر t> 0 به صورت زیر است:
حال مقدار t مثبتی که e ( t2/2 ) - ta را حداقل می کند، مقداری است که ( t2/2 ) - ta را حداقل می کند، یعنی t=a است؛ بنابراین برای a> 0 داریم:
حال مثالی از کاربرد این کران را نشان می دهیم. فرض کنیم X1, … , Xn متغیرهای تصادفی مستقل با توزیع برنولی باشند، که هر کدام دارای احتمال p > 1/2 باشند، احتمال رخداد همزمان بیش از n/2 متغیر تصادفی { X k = 1 } برابر است با
کران چرنوف نشان می دهد که رابطهٔ بالا دارای کران پایین زیر است:
توجه کنید که برای تعدادی نمونهٔ تصادفی با توزیع برنولی داریم μ = n p با استفاده از نتایج کران چرنوف ( در ادامه ) می توان نشان داد که
باید توجه کرد که با توجه به خواسته های مسئله می توان از فرم های مختلفی از کران چرنوف استفاده کرد.
تصور کنید سکه ای اریب داریم ( یعنی احتمال رو و پشت با هم یکسان نباشند ) . اکنون سؤال این است که چطور می توان سمتی که دارای احتمال بیشتری است را پیدا؟ جواب ساده این است که سکه را بی نهایب بار پرتاب می کنیم و با حساب کردن احتمال هر سمت، آنی که احتمال بیشتری دارد را انتخاب می کنیم؛ ولی در عمل چنین کاری انکانپذیر نیست. چگونه می توان با تعداد پرتاپ های محدود، با احتمالی خوب، حدسی در مورد احتمال سمتی که دارای احتمال رو/پشت بیشتر زد؟

wiki: کران چرنوف
