در مخابرات، کد همینگ، کد تصحیح خطای خطی می باشد که به افتخار ریچارد همینگ، مخترع آن گذاشته شده است. کدهای همینگ می توانند همزمان ۲ بیت خطا را شناسایی کنند و ۱ بیت خطا را تصحیح کنند؛ از طرفی parity code به تنهایی نمی تواند خطاها را تصحیح کند و فقط فرد تعداد بیت از خطاها را تشخیص می دهد. [ ۱] ریچارد همینگ، این متد را در سال ۱۹۵۰ ابداع کرد به عنوان روشی که تصحیح خطا را به صورت اتوماتیک انجام می داد؛ او در مقالهٔ اصلی خود، کدهای همینگ ( ۷٬۴ ) را مورد بررسی قرار می دهد که سه بیت توازن ( parity ) به دادهٔ چهار بیتی اضافه می کند. [ ۱]
از لحاظ ریاضی، کدهای همینگ کلاسی از کدهای خطی باینری هستند.
برای هر عدد صحیح r ≥ ۲ وجود دارد کدی ( Block length ) با طول n = 2r − ۱ پیامی ( Message length ) به طول k = 2r − r − ۱. از این رو برآورد ما از متد همینگ اینگونه به دست می آید: ( R = k / n = ۱ − r / ( 2r − ۱ یعنی بیشترین احتمال برای کدهایی است که در کمترین فاصله از سه هستند. ( کمترین تعداد بیت هایی که باید تغییر کنند تا از کدی، کد معتبر دیگری تولید کنیم، سه بیت است )
ماتریس سنجش توازن ( parity - check matrix ) برای کدهای همینگ از تمام ستون های به طول r ناصفر ساخته می شود؛ ستون های این ماتریس دوبه دو مستقل خطی هستند.
در این روش بیت های کمی به دیتاها اضافه می شود؛ که این یعنی همینگ کد به شرط کم بودن خطا در داده ها، می تواند خطاها را تشخیص داده و تصحیح کند. از کاربردهای این روش می توان به حافظهٔ کامپیوتر ECC memory اشاره کرد؛ وقتی که بیت خطاها بسیار کم باشند، کدهای همینگ آن را مدیریت می کنند.
در نتیجه مخابره قابل اطمینان در صورتی که فاصله همینگ بین رشته بیت فرستنده و گیرنده یک یا کمتر از یک باشد، ممکن می شود.
دسته ای از کدها برای تشخیص و تصحیح خطا در ارسال اطلاعات استفاده می شوند؛ که به آنها کد همینگ می گویند. در این کدها حداقل اختلافی که بین دو کد نمایشی وجود دارد فاصله همینگ نامند.
ما در اینجا کد همینگ با حداقل فاصله ۳ را توضیح می دهیم. یعنی بیتهایی را که به آنها اضافه می کنیم ۳ بیت می باشد. چون در کد همینگ به منظور تشخیص و تصحیح خطا باید بیتهایی را به کدمان اضافه کنیم.
اگر بخواهیم کد NBCD را با حداقل فاصله ۳ ارسال کنیم. باید به کد NBCD، سه بیت اضافه کنیم؛ که اطلاعات ارسالی به صورت زیر می شود. C1 c2 b3 c4 b5 b6 b7 که در اینجا بیت c1 و c2 و c4 سه بیتی هستند که به کدمان اضافه می شوند و به آنها بیتهای الحاقی می گویند و به بیتهای b3 و b5 و b6 و b7 بیتهای اطلاعاتی می گویند.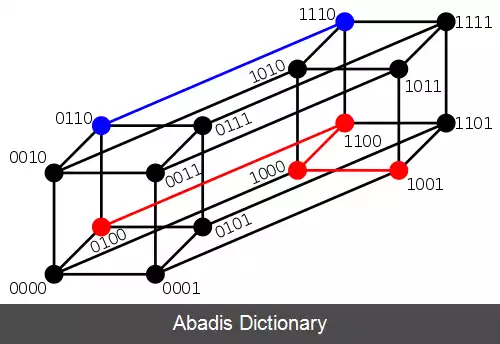
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز لحاظ ریاضی، کدهای همینگ کلاسی از کدهای خطی باینری هستند.
برای هر عدد صحیح r ≥ ۲ وجود دارد کدی ( Block length ) با طول n = 2r − ۱ پیامی ( Message length ) به طول k = 2r − r − ۱. از این رو برآورد ما از متد همینگ اینگونه به دست می آید: ( R = k / n = ۱ − r / ( 2r − ۱ یعنی بیشترین احتمال برای کدهایی است که در کمترین فاصله از سه هستند. ( کمترین تعداد بیت هایی که باید تغییر کنند تا از کدی، کد معتبر دیگری تولید کنیم، سه بیت است )
ماتریس سنجش توازن ( parity - check matrix ) برای کدهای همینگ از تمام ستون های به طول r ناصفر ساخته می شود؛ ستون های این ماتریس دوبه دو مستقل خطی هستند.
در این روش بیت های کمی به دیتاها اضافه می شود؛ که این یعنی همینگ کد به شرط کم بودن خطا در داده ها، می تواند خطاها را تشخیص داده و تصحیح کند. از کاربردهای این روش می توان به حافظهٔ کامپیوتر ECC memory اشاره کرد؛ وقتی که بیت خطاها بسیار کم باشند، کدهای همینگ آن را مدیریت می کنند.
در نتیجه مخابره قابل اطمینان در صورتی که فاصله همینگ بین رشته بیت فرستنده و گیرنده یک یا کمتر از یک باشد، ممکن می شود.
دسته ای از کدها برای تشخیص و تصحیح خطا در ارسال اطلاعات استفاده می شوند؛ که به آنها کد همینگ می گویند. در این کدها حداقل اختلافی که بین دو کد نمایشی وجود دارد فاصله همینگ نامند.
ما در اینجا کد همینگ با حداقل فاصله ۳ را توضیح می دهیم. یعنی بیتهایی را که به آنها اضافه می کنیم ۳ بیت می باشد. چون در کد همینگ به منظور تشخیص و تصحیح خطا باید بیتهایی را به کدمان اضافه کنیم.
اگر بخواهیم کد NBCD را با حداقل فاصله ۳ ارسال کنیم. باید به کد NBCD، سه بیت اضافه کنیم؛ که اطلاعات ارسالی به صورت زیر می شود. C1 c2 b3 c4 b5 b6 b7 که در اینجا بیت c1 و c2 و c4 سه بیتی هستند که به کدمان اضافه می شوند و به آنها بیتهای الحاقی می گویند و به بیتهای b3 و b5 و b6 و b7 بیتهای اطلاعاتی می گویند.

wiki: کد همینگ
