در یادگیری ماشین و آمار کاهش بعد یا کاهش ابعاد به معنی انتقال داده از فضای با بعد بیش تر به فضایی با بعد پایین تر به شکل تحت نظر ( Supervised ) [ ۱] است، به گونه ای که داده در فضای با بعد کمتر بتواند به طور معنی داری داده اصلی را نمایندگی کند و ویژگی های آن را در خود داشته باشد. کار با داده در ابعاد بالا می تواند به دلایل گوناگونی نامطلوب باشد؛ داده در ابعاد بالا به دلیل نفرین ابعاد بسیار تنک باشد و همچنین تحلیل داده در ابعاد بالا از لحاظ محاسباتی بسیار کند و پرهزینه است. کاهش ابعاد در شاخه هایی که با تعداد زیادی مشاهده و/یا تعداد زیادی ویژگی سروکار دارند مانند پردازش سیگنال یا بینایی ماشین به کار می رود. کاهش ابعاد را می توان به انتخاب ویژگی و استخراج ویژگی تقسیم کرد. [ ۲]
هدف نهایی انتخاب ویژگی این است که زیر مجموعه ای از ویژگی ها در فضای اصلی را انتخاب کند که حاوی بیش ترین اطلاعات موجود در داده های اصلی باشند؛ سپس این ویژگی ها را به عنوان ویژگی در بعد کاهش یافته معرفی کند. سه روش کلی انتخاب ویژگی شامل پالایش ( برای مثال کسب اطلاعات ) ، روش پوشه ( برای مثال جست و جو بر اساس دقت ) و روش جاسازی شده ( حذف یا افزودن ویژگی ها بر اساس خطای تخمین ) هستند.
برخی از وظایف معمول تحلیل داده مانند خوشه بندی و رگرسیون در فضای کاهش یافته به این روش بهتر و دقیق تر عمل می کنند. [ ۳]
استخراج ویژگی داده ها را در فضای با ابعاد بزرگ به یک فضای ابعاد کمتر تبدیل می کند. تبدیل داده ها می تواند به شکل خطی باشد، ( مانند روش تحلیل مولفه اصلی ) اما همچنین بسیاری از تکنیک های کاهش ابعاد غیر خطی نیز وجود دارد. [ ۴] [ ۵] روش های غیر خطی معمولاً ساده تر و سریع ترند اما به خصوص برای داده های پیچیده روش های غیر خطی دقت بیش تری دارند. [ ۶] برای داده های چند بعدی، نماینده تانسور را می توان در کاهش ابعاد از طریق یادگیری زیر فضای چندخطی استفاده کرد. [ ۷]
مقاله اصلی: تحلیل مولفه های اصلی
این روش اصلی ترین روش خطی برای کاهش ابعاد است؛ این روش نگاشت خطی داده ها را به یک فضا با بعد پایین تر انجام می دهد، به طوری که میزان توضیح واریانس داده اصلی در داده منتقل شده ( به ابعاد کمتر ) بیشینه باشد. در عمل، ماتریس واریانس ( و بعضی اوقات کوواریانس ) داده ها ساخته می شود و بردار ویژه این ماتریس محاسبه می شود. بردارویژه هایی که متناظر با بزرگ ترین مقادیر ویژه ها هستند، بیش ترین میزان اطلاعات از داده های اصلی را در خود دارند و اکنون می توانند برای بازسازی بخش بزرگی از واریانس داده های اصلی استفاده شوند. به صورت تخمینی، چندین بردار اول را می توان نماینده رفتار کلان داده تفسیر کرد. داده در ابعاد کمتر با استفاده از این بردارهای اصلی همراه با از دست دادن بخشی از اطلاعات ( با این امید که توضیح دهندگی واریانس را تا حد خوبی حفظ کند ) ساخته می شود.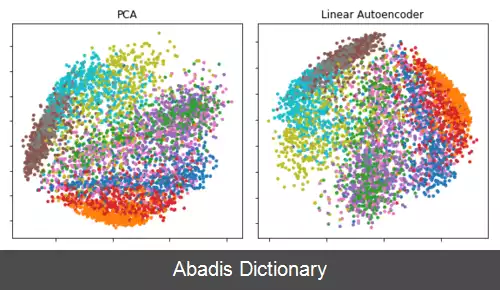
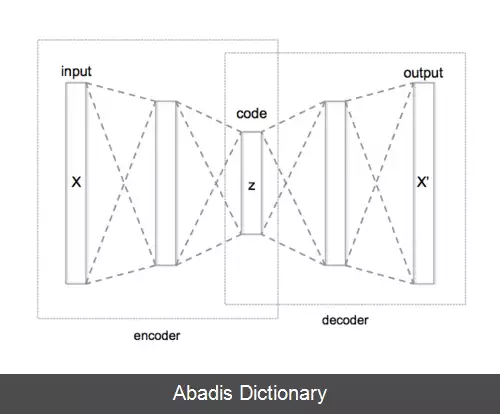
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهدف نهایی انتخاب ویژگی این است که زیر مجموعه ای از ویژگی ها در فضای اصلی را انتخاب کند که حاوی بیش ترین اطلاعات موجود در داده های اصلی باشند؛ سپس این ویژگی ها را به عنوان ویژگی در بعد کاهش یافته معرفی کند. سه روش کلی انتخاب ویژگی شامل پالایش ( برای مثال کسب اطلاعات ) ، روش پوشه ( برای مثال جست و جو بر اساس دقت ) و روش جاسازی شده ( حذف یا افزودن ویژگی ها بر اساس خطای تخمین ) هستند.
برخی از وظایف معمول تحلیل داده مانند خوشه بندی و رگرسیون در فضای کاهش یافته به این روش بهتر و دقیق تر عمل می کنند. [ ۳]
استخراج ویژگی داده ها را در فضای با ابعاد بزرگ به یک فضای ابعاد کمتر تبدیل می کند. تبدیل داده ها می تواند به شکل خطی باشد، ( مانند روش تحلیل مولفه اصلی ) اما همچنین بسیاری از تکنیک های کاهش ابعاد غیر خطی نیز وجود دارد. [ ۴] [ ۵] روش های غیر خطی معمولاً ساده تر و سریع ترند اما به خصوص برای داده های پیچیده روش های غیر خطی دقت بیش تری دارند. [ ۶] برای داده های چند بعدی، نماینده تانسور را می توان در کاهش ابعاد از طریق یادگیری زیر فضای چندخطی استفاده کرد. [ ۷]
مقاله اصلی: تحلیل مولفه های اصلی
این روش اصلی ترین روش خطی برای کاهش ابعاد است؛ این روش نگاشت خطی داده ها را به یک فضا با بعد پایین تر انجام می دهد، به طوری که میزان توضیح واریانس داده اصلی در داده منتقل شده ( به ابعاد کمتر ) بیشینه باشد. در عمل، ماتریس واریانس ( و بعضی اوقات کوواریانس ) داده ها ساخته می شود و بردار ویژه این ماتریس محاسبه می شود. بردارویژه هایی که متناظر با بزرگ ترین مقادیر ویژه ها هستند، بیش ترین میزان اطلاعات از داده های اصلی را در خود دارند و اکنون می توانند برای بازسازی بخش بزرگی از واریانس داده های اصلی استفاده شوند. به صورت تخمینی، چندین بردار اول را می توان نماینده رفتار کلان داده تفسیر کرد. داده در ابعاد کمتر با استفاده از این بردارهای اصلی همراه با از دست دادن بخشی از اطلاعات ( با این امید که توضیح دهندگی واریانس را تا حد خوبی حفظ کند ) ساخته می شود.


wiki: کاهش ابعاد
