چهارضلعی ساکری ( Saccheri Quadrilateral ) ( که به چهارضلعی خیام - ساکِری نیز معروف است ) ، را نخستین بار عمر خیّام مورد بحث قرار داد اما در غرب با کارهای ساکری معرفی شد. خیام این چهارضلعی را بیش از هفت سده قبل از ساکری در کتاب «شرح ما اشکل» مطرح کرده است. ساکری ریاضیدان ایتالیایی و نویسنده کتاب «اقلیدس به دور از همهٔ نارسایی ها» ( اقلیدس عاری از هرگونه تناقض ) در سال ۱۷۷۳ بود.
هندسه ای که اقلیدس بنا نهاد بر پنج اصل موضوع ( بنداشت ) بنا شده است. ریاضیدانان حتی قبل از تدوین این اصول توسط اقلیدس، بر سر چهار اصل نخست توافق داشتند امّا اصلِ پنجم از همان دوران تا هنگامی که در اواخر قرن هفدهم با ظهور هندسه های نااقلیدسی برای همیشه حل شود؛ مورد مناقشه بود. ریاضی دانان تلاش می کردند اصل پنجم را که به نظرشان پیچیده می آمد با توجه به چهار اصل نخست به عنوان یک "قضیه"ای مانند سایر قضایا، "اثبات" کنند. جیرولامو ساکری تلاش کرد با طرح یک چهار ضلعی، از طریق برهان خلف این اصل را از چهار اصل قبلی نتیجه بگیرد. او برای اثبات اصل پنجم از روی چهار اصل اوّل، و بیست و هشت قضیهٔ منتج از آن ها، ( هندسهٔ نتاری یا هندسه بیطرف ) چهار ضلعی ای را در نظر گرفت که زوایای A و B قائمه و اضلاع AD و BC برابرند. ساکری با رسم قطر AC و BD و با استفاده از قضایای هم نهشتی ساده ( از بین بیست و هشت قضیهٔ اول ) به آسانی نشان داد که زاویه C و D برابر هستند. بنابراین سه امکان پیش می آید زوایای C و D حاده باشند، قائمه باشند یا منفرجه باشند.
ساکِری با توجه به اصل دوم اقلیدس که خط را نامحدود می داند به سادگی اثبات کرد که حالت منفرجه غیرممکن است. ( بعدها ریمان با جایگزین کردن اصل دیگری به جای اصل دوم که خط را محدود اما بی کرانه برمی شمارد هندسهٔ ریمانی را به وجود آورد. ) اما برای اثبات نادرستی حالت حادّه، دچار دردسر زیادی شد و سرانجام از روی عجز اعلام کرد "فرضِ زاویهٔ حادّه، مطلقاً غلط است، زیرا که این فرض، با ذاتِ خط مستقیم، ناسازگار می باشد!" در نتیجه "تصور کرد" توانسته است با کمک برهان خلف، اصل توازی را از چهار اصل نخست، نتیجه بگیرد. اگر ساکری اینقدر مشتاقانه در جهتِ اثباتِ نادرستیِ فرضِ حالتِ حادّه تلاش نکرده بود، می توانست یک سده قبل از لباچفسکی و بویویی نوعی از هندسهٔ نااقلیدسی که امروز به آن هندسهٔ هذلولوی یا هندسهٔ لباچفسکی گفته می شود را ابداع کند.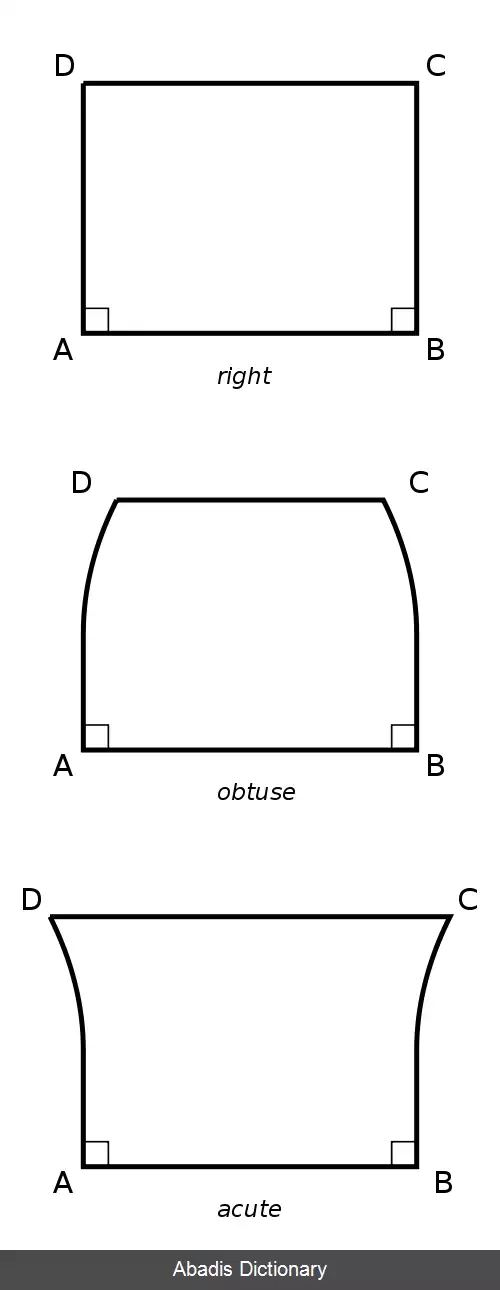

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهندسه ای که اقلیدس بنا نهاد بر پنج اصل موضوع ( بنداشت ) بنا شده است. ریاضیدانان حتی قبل از تدوین این اصول توسط اقلیدس، بر سر چهار اصل نخست توافق داشتند امّا اصلِ پنجم از همان دوران تا هنگامی که در اواخر قرن هفدهم با ظهور هندسه های نااقلیدسی برای همیشه حل شود؛ مورد مناقشه بود. ریاضی دانان تلاش می کردند اصل پنجم را که به نظرشان پیچیده می آمد با توجه به چهار اصل نخست به عنوان یک "قضیه"ای مانند سایر قضایا، "اثبات" کنند. جیرولامو ساکری تلاش کرد با طرح یک چهار ضلعی، از طریق برهان خلف این اصل را از چهار اصل قبلی نتیجه بگیرد. او برای اثبات اصل پنجم از روی چهار اصل اوّل، و بیست و هشت قضیهٔ منتج از آن ها، ( هندسهٔ نتاری یا هندسه بیطرف ) چهار ضلعی ای را در نظر گرفت که زوایای A و B قائمه و اضلاع AD و BC برابرند. ساکری با رسم قطر AC و BD و با استفاده از قضایای هم نهشتی ساده ( از بین بیست و هشت قضیهٔ اول ) به آسانی نشان داد که زاویه C و D برابر هستند. بنابراین سه امکان پیش می آید زوایای C و D حاده باشند، قائمه باشند یا منفرجه باشند.
ساکِری با توجه به اصل دوم اقلیدس که خط را نامحدود می داند به سادگی اثبات کرد که حالت منفرجه غیرممکن است. ( بعدها ریمان با جایگزین کردن اصل دیگری به جای اصل دوم که خط را محدود اما بی کرانه برمی شمارد هندسهٔ ریمانی را به وجود آورد. ) اما برای اثبات نادرستی حالت حادّه، دچار دردسر زیادی شد و سرانجام از روی عجز اعلام کرد "فرضِ زاویهٔ حادّه، مطلقاً غلط است، زیرا که این فرض، با ذاتِ خط مستقیم، ناسازگار می باشد!" در نتیجه "تصور کرد" توانسته است با کمک برهان خلف، اصل توازی را از چهار اصل نخست، نتیجه بگیرد. اگر ساکری اینقدر مشتاقانه در جهتِ اثباتِ نادرستیِ فرضِ حالتِ حادّه تلاش نکرده بود، می توانست یک سده قبل از لباچفسکی و بویویی نوعی از هندسهٔ نااقلیدسی که امروز به آن هندسهٔ هذلولوی یا هندسهٔ لباچفسکی گفته می شود را ابداع کند.


wiki: چهارضلعی ساکری
