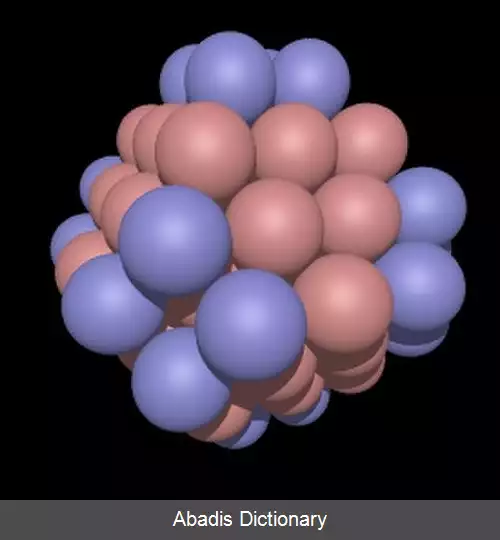
در هندسه ، چندوجهی واترمن ( به انگلیسی: Waterman polyhedron ) خانواده ای از چندوجهی ها است که در حدود سال ١٩٩٠ توسط ریاضیدان استیو واترمن کشف شد. چند وجهی واترمن با بسته بندی کره ها بر اساس شبکه کریستالی هگزاگونال فشرده ( fcc ) یا ( CPP ) ایجاد می شود سپس کره هایی را که دورتر از یک شعاع مشخص هستند، از بین می برد، [ ۱] سپس پوش محدب مراکز کره ایجاد می شود.
چند وجهی واترمن خانواده وسیعی از چند وجهی را تشکیل می دهد. بعضی از آنها دارای چندین ویژگی مانند تقارن های متعدد یا چندوجهی های متحدالشکل هستند. برخی دیگر فقط مجموعه ای از وجوه هستند که از چند ضلعی های محدب غیر متحدالشکل تشکیل شده اند.
معروف ترین چند وجهی های واترمن آنهایی هستند که دارای مراکز در نقطه ( 0، 0، 0 ) هستند و از صدها چند ضلعی ساخته شده اند. چنین چند وجهی ها شبیه کره ها هستند. در حقیقت ، هرچه وجوه چندوجهی واترمن بیشتر باشد ، از نظر حجم و مساحت کل به کره محیطی آن نزدیکتر است.
با هر نقطه از فضای سه بعدی می توانیم خانواده ای از چند وجهی واترمن را با مقادیر مختلف شعاع کره های محدود شده به دست آوریم. بنابراین ، از نظر ریاضی می توانیم چند وجهی واترمن را به عنوان فضاهای 4 بعدی ( W ( x ، y ، z ، r در نظر بگیریم ، که x ، y ، z مختصات یک نقطه در فضلی سه بعدی بوده ، و r یک عدد مثبت بزرگتر از ١ است. [ ۲]
می تواند هفت منشأ در CCP تعریف شود[ ۳] ، که {… ، ٣ ، ٢ ، ١}=n باشد:
• منشأ ١: offset 0, 0, 0, radius sqrt ( 2n )
• منشأ ٢: offset 1/2, 1/2, 0, radius sqrt ( 2+4n ) /2
• منشأ ٣: offset 1/3, 1/3, 2/3, radius sqrt ( 6 ( n+1 ) ) /3
• منشأ ٣*: offset 1/3, 1/3, 1/3, radius sqrt ( 3+6n ) /3
• منشأ ٤: offset 1/2, 1/2, 1/2, radius sqrt ( 3+8 ( n - 1 ) ) /2
• منشأ ٥: offset 0, 0, 1/2, radius sqrt ( 1+4n ) /2
• منشأ ٦: offset 1, 0, 0, radius sqrt ( 1+2 ( n - 1 ) )
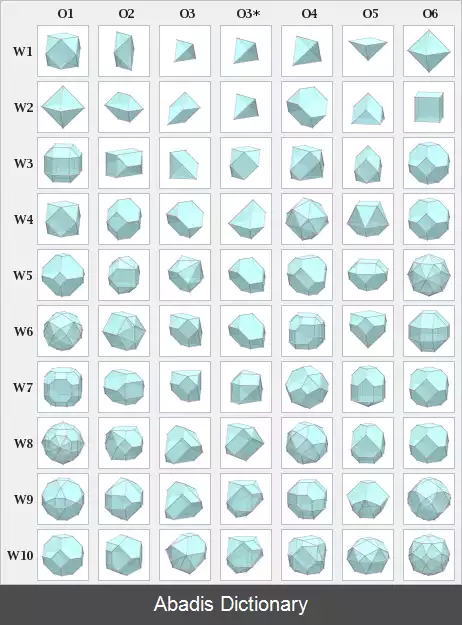
بسته به منشأ از بین بردن کره ها ، شکل متفاوت و چند وجهی حاصل از آن بدست می آید.
برخی از چندوجهی های واترمن اجسام افلاطونی و ارشمیدسی را ایجاد می کنند. برای این مقایسه چند وجهی واترمن آنها نرمال می شوند ، به عنوان مثال حجم و اندازه W2 O1 متفاوت از W1 O6 است ، اما شکل هر دو یک هشت وجهی است.
• چهاروجهی: W1 O3*, W2 O3*, W1 O3, W1 O4
• هشت وجهی: W2 O1, W1 O6
• مکعب: W2 O6
• هیچ چندوجهی واترمنی به شکل دوازده وجهی یا بیست وجهی نیست.


این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفچند وجهی واترمن خانواده وسیعی از چند وجهی را تشکیل می دهد. بعضی از آنها دارای چندین ویژگی مانند تقارن های متعدد یا چندوجهی های متحدالشکل هستند. برخی دیگر فقط مجموعه ای از وجوه هستند که از چند ضلعی های محدب غیر متحدالشکل تشکیل شده اند.
معروف ترین چند وجهی های واترمن آنهایی هستند که دارای مراکز در نقطه ( 0، 0، 0 ) هستند و از صدها چند ضلعی ساخته شده اند. چنین چند وجهی ها شبیه کره ها هستند. در حقیقت ، هرچه وجوه چندوجهی واترمن بیشتر باشد ، از نظر حجم و مساحت کل به کره محیطی آن نزدیکتر است.
با هر نقطه از فضای سه بعدی می توانیم خانواده ای از چند وجهی واترمن را با مقادیر مختلف شعاع کره های محدود شده به دست آوریم. بنابراین ، از نظر ریاضی می توانیم چند وجهی واترمن را به عنوان فضاهای 4 بعدی ( W ( x ، y ، z ، r در نظر بگیریم ، که x ، y ، z مختصات یک نقطه در فضلی سه بعدی بوده ، و r یک عدد مثبت بزرگتر از ١ است. [ ۲]
می تواند هفت منشأ در CCP تعریف شود[ ۳] ، که {… ، ٣ ، ٢ ، ١}=n باشد:
• منشأ ١: offset 0, 0, 0, radius sqrt ( 2n )
• منشأ ٢: offset 1/2, 1/2, 0, radius sqrt ( 2+4n ) /2
• منشأ ٣: offset 1/3, 1/3, 2/3, radius sqrt ( 6 ( n+1 ) ) /3
• منشأ ٣*: offset 1/3, 1/3, 1/3, radius sqrt ( 3+6n ) /3
• منشأ ٤: offset 1/2, 1/2, 1/2, radius sqrt ( 3+8 ( n - 1 ) ) /2
• منشأ ٥: offset 0, 0, 1/2, radius sqrt ( 1+4n ) /2
• منشأ ٦: offset 1, 0, 0, radius sqrt ( 1+2 ( n - 1 ) )
بسته به منشأ از بین بردن کره ها ، شکل متفاوت و چند وجهی حاصل از آن بدست می آید.
برخی از چندوجهی های واترمن اجسام افلاطونی و ارشمیدسی را ایجاد می کنند. برای این مقایسه چند وجهی واترمن آنها نرمال می شوند ، به عنوان مثال حجم و اندازه W2 O1 متفاوت از W1 O6 است ، اما شکل هر دو یک هشت وجهی است.
• چهاروجهی: W1 O3*, W2 O3*, W1 O3, W1 O4
• هشت وجهی: W2 O1, W1 O6
• مکعب: W2 O6
• هیچ چندوجهی واترمنی به شکل دوازده وجهی یا بیست وجهی نیست.





wiki: چندوجهی واترمن
