یک چندوجهی منتظم، چندوجهی است که گروه تقارن آن بر روی پرچم های آن به صورت ترایا رفتار می کند. یک چندوجهی منتظم، کاملاً متقارن بوده و همزمان یال - متقارن، رأس - متقارن و وجه - متقارن است. در متون کلاسیک، تعریف های معادل مختلفی برای چندوجهی منتظم بیان شده که یکی از متداول ترین آنها به صورت زیر است: «چندوجهی منتظم چندوجهی است که وجه های آن چندضلعی های منتظم هم نهشت بوده که به صورت یکسان به دور هر رأس قرار گرفته اند. »
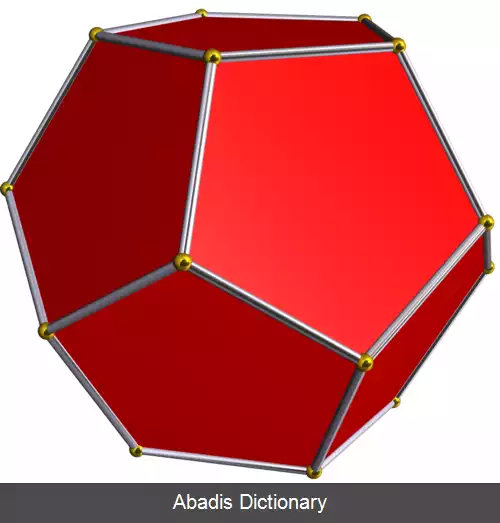
یک چندوجهی منتظم با نماد شلفلی {n, m} نشان داده می شود، که n تعداد اضلاع هر وجه و m تعداد وجه هایی است که در هر رأس به یکدیگر می رسند. ۵ چندوجهی منتظم کوژ متناهی وجود دارند که با عنوان اجسام افلاطونی شناخته می شوند. این چندوجهی ها عبارتند از چهاروجهی {۳، ۳}، مکعب {۳، ۴}، هشت وجهی {۴، ۳}، دوازده وجهی {۳، ۵} و بیست وجهی {۵، ۳}. همچنین با در نظر گرفتن ۴ چندوجهی ستاره ای منتظم ( چندوجهی کپلر–پوآنسو ) ، در مجموع ۹ چندوجهی منتظم مختلف وجود دارند.
۵ چندوجهی منتظم کوژ وجود دارند که با عنوان اجسام افلاطونی شناخته می شوند و ۴ چندوجهی منتظم ستاره ای وجود دارند که با نام چندوجهی های کپلر - پوآنسو شناخته می شوند. [ ۱]
مشخصه اولر اجسام افلاطونی، ۲ است.




این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک چندوجهی منتظم با نماد شلفلی {n, m} نشان داده می شود، که n تعداد اضلاع هر وجه و m تعداد وجه هایی است که در هر رأس به یکدیگر می رسند. ۵ چندوجهی منتظم کوژ متناهی وجود دارند که با عنوان اجسام افلاطونی شناخته می شوند. این چندوجهی ها عبارتند از چهاروجهی {۳، ۳}، مکعب {۳، ۴}، هشت وجهی {۴، ۳}، دوازده وجهی {۳، ۵} و بیست وجهی {۵، ۳}. همچنین با در نظر گرفتن ۴ چندوجهی ستاره ای منتظم ( چندوجهی کپلر–پوآنسو ) ، در مجموع ۹ چندوجهی منتظم مختلف وجود دارند.
۵ چندوجهی منتظم کوژ وجود دارند که با عنوان اجسام افلاطونی شناخته می شوند و ۴ چندوجهی منتظم ستاره ای وجود دارند که با نام چندوجهی های کپلر - پوآنسو شناخته می شوند. [ ۱]
مشخصه اولر اجسام افلاطونی، ۲ است.






wiki: چندوجهی منتظم
