یک چندضلعی ستاره ای منظم، یک چندضلعی منتظم غیرمحدب است. در ریاضیات، تنها چندضلعی های ستاره ای منتظم مورد مطالعه قرار گرفته اند و چندضلعی های ستاره ای عمومی ( غیرمنتظم ) ، به صورت رسمی تعریف نشده اند.
در هندسه، یک چندضلعی ستاره ای منتظم، چندضلعی است که اضلاع آن یکدیگر را قطع می کنند، اندازه اضلاع و زوایای داخلی آن برابر بوده و با اتصال یک رأس یک چندضلعی p - وجهی منتظم ساده به یک رأس غیرمجاور و ادامه دادن این روند تا رسیدن دوباره به همان رأس ایجاد می شود. [ ۲] در یک چندضلعی ستاره ای، هر ضلع آن تنها دو ضلع دیگر را قطع می کند. برای اعداد صحیح p و q، این چندضلعی می تواند با اتصال هر نقطهٔ qام از p نقطه که به فاصله یکسان بر روی یک دایره قرار گرفته اند، ایجاد شود. [ ۳] نماد چنین چندضلعی {p/q} بوده که معادل {p/p - q} است. چندضلعی های ستاره ای منتظم زمانی ایجاد خواهند شد که p و q متباین باشند.
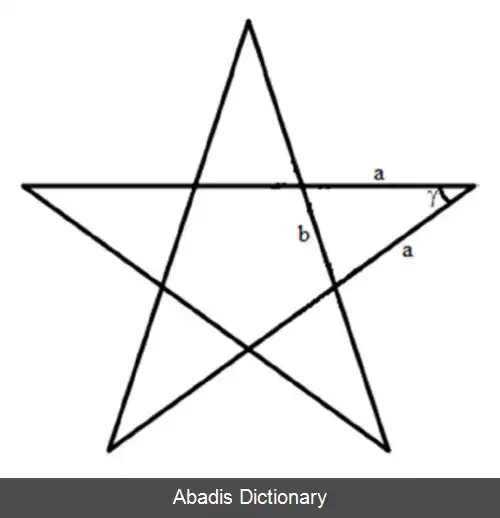
مساحت هر ستارۀ n پر منتظم، برابر با مجموع مساحت چندضلعی مولد آن و مساحت مثلث های اطراف آن است. به عنوان مثال، ستارۀ منتظم پنج پر زیر را در نظر بگیرید. مساحت ستاره در این حالت برابر است با:
A s t a r = A p o l y g o n + n × ( A t r i a n g l e ) = n b 2 4 t a n ( π / n ) + n a 2 2 s i n ( γ )
برای تبدیل طول ضلع چندضلعی به طول ضلع مثلث ( پر ستاره ) می توانیم از قانون کسینوس ها استفاده کنیم:
b 2 = a 2 + a 2 − 2 a 2 c o s γ = 2 a 2 ( 1 − c o s γ )
با جایگذاری این عبارت در فرمول مساحت ستاره، خواهیم داشت:
A s t a r = n a 2 ( 1 − c o s γ ) 2 t a n ( π / n ) + n a 2 s i n γ 2 = n a 2 2 ( 1 − c o s γ t a n ( π / n ) + s i n γ )
با محاسبات جمع زوایای داخلی مثلث و زوایای داخلی چندضلعی می دانیم:
γ = π − 4 π n
فلذا مقادیر سینوس و کسینوس گاما را می توان به شکل زیر ساده سازی کرد:
s i n γ = s i n ( π − 4 π n ) = s i n ( 4 π n )
c o s γ = c o s ( π − 4 π n ) = − c o s ( 4 π n )
اگر این مقادیر را در فرمول مساحت ستاره قرار دهیم:
A s t a r = n a 2 2
با گرفتن مخرج مشترک و ساده سازی عبارت داخل کروشه به فرمول زیر خواهیم رسید: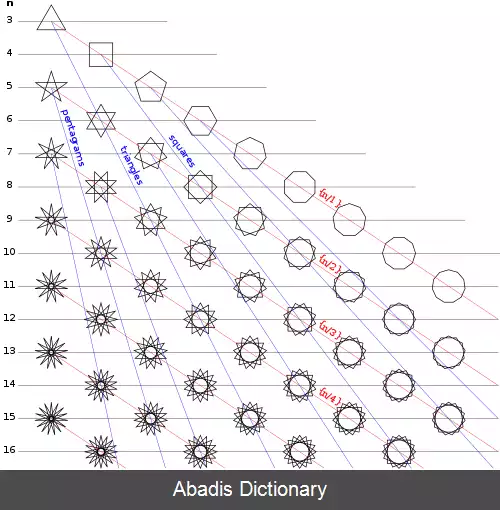
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر هندسه، یک چندضلعی ستاره ای منتظم، چندضلعی است که اضلاع آن یکدیگر را قطع می کنند، اندازه اضلاع و زوایای داخلی آن برابر بوده و با اتصال یک رأس یک چندضلعی p - وجهی منتظم ساده به یک رأس غیرمجاور و ادامه دادن این روند تا رسیدن دوباره به همان رأس ایجاد می شود. [ ۲] در یک چندضلعی ستاره ای، هر ضلع آن تنها دو ضلع دیگر را قطع می کند. برای اعداد صحیح p و q، این چندضلعی می تواند با اتصال هر نقطهٔ qام از p نقطه که به فاصله یکسان بر روی یک دایره قرار گرفته اند، ایجاد شود. [ ۳] نماد چنین چندضلعی {p/q} بوده که معادل {p/p - q} است. چندضلعی های ستاره ای منتظم زمانی ایجاد خواهند شد که p و q متباین باشند.
مساحت هر ستارۀ n پر منتظم، برابر با مجموع مساحت چندضلعی مولد آن و مساحت مثلث های اطراف آن است. به عنوان مثال، ستارۀ منتظم پنج پر زیر را در نظر بگیرید. مساحت ستاره در این حالت برابر است با:
A s t a r = A p o l y g o n + n × ( A t r i a n g l e ) = n b 2 4 t a n ( π / n ) + n a 2 2 s i n ( γ )
برای تبدیل طول ضلع چندضلعی به طول ضلع مثلث ( پر ستاره ) می توانیم از قانون کسینوس ها استفاده کنیم:
b 2 = a 2 + a 2 − 2 a 2 c o s γ = 2 a 2 ( 1 − c o s γ )
با جایگذاری این عبارت در فرمول مساحت ستاره، خواهیم داشت:
A s t a r = n a 2 ( 1 − c o s γ ) 2 t a n ( π / n ) + n a 2 s i n γ 2 = n a 2 2 ( 1 − c o s γ t a n ( π / n ) + s i n γ )
با محاسبات جمع زوایای داخلی مثلث و زوایای داخلی چندضلعی می دانیم:
γ = π − 4 π n
فلذا مقادیر سینوس و کسینوس گاما را می توان به شکل زیر ساده سازی کرد:
s i n γ = s i n ( π − 4 π n ) = s i n ( 4 π n )
c o s γ = c o s ( π − 4 π n ) = − c o s ( 4 π n )
اگر این مقادیر را در فرمول مساحت ستاره قرار دهیم:
A s t a r = n a 2 2
با گرفتن مخرج مشترک و ساده سازی عبارت داخل کروشه به فرمول زیر خواهیم رسید:


wiki: چندضلعی ستاره ای
