چندضلعی ایزوتتیک ( Isothetic Polygon ) ، چندضلعی است که ضلع های متناظر آن دو خانواده پارامتری از خطوط راست هستند که مداد خطوط با مراکز در دو نقطه ( احتمالاً نقطه در بی نهایت ) نامید می شود.
معروف ترین مثال برای چندضلعی های ایزوتتیک چند ضلعی های متعامد هستند که سابقاً به عنوان یک مترادف استفاده می شد.
این اصطلاح از ریشه یونانی iso ( همانند – یکسان – مشابه ) و thetos ( مکان – موقعیت ) گرفته شده و به طور کلی به معنای چند ضلعی با مکان مشترک برای ضلع هاست.
این اصطلاح برای اولین بار در سالهای ابتدایی هندسه محاسباتی مطرح شد.
در ابتدا تأکید بر ارائه الگوریتم کارامد برای چند ضلعی های متعامد بود تا اینکه کاربرد چند ضلعی های ایزوتتیک در ارائه شکل های برای طراحی و ساخت مدارهای مجتمع مطرح شد.
زمانی که مشخص شد کارآمدی الگوریتم های هندسه برای چندضلعی های متعامد دیگر به این بستگی ندارد که اضلاع حتماً یکدیگر را در زاویه قائمه ببینند بلکه اضلاع به طور طبیعی به دو مجموعه متناوب ( بخش های عمودی و افقی ) تقسیم می شوند.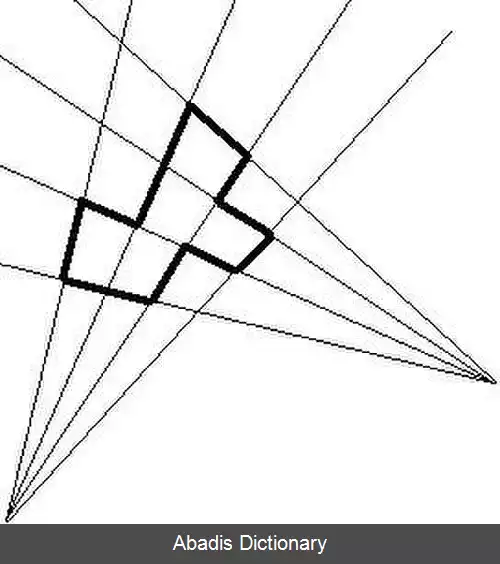
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمعروف ترین مثال برای چندضلعی های ایزوتتیک چند ضلعی های متعامد هستند که سابقاً به عنوان یک مترادف استفاده می شد.
این اصطلاح از ریشه یونانی iso ( همانند – یکسان – مشابه ) و thetos ( مکان – موقعیت ) گرفته شده و به طور کلی به معنای چند ضلعی با مکان مشترک برای ضلع هاست.
این اصطلاح برای اولین بار در سالهای ابتدایی هندسه محاسباتی مطرح شد.
در ابتدا تأکید بر ارائه الگوریتم کارامد برای چند ضلعی های متعامد بود تا اینکه کاربرد چند ضلعی های ایزوتتیک در ارائه شکل های برای طراحی و ساخت مدارهای مجتمع مطرح شد.
زمانی که مشخص شد کارآمدی الگوریتم های هندسه برای چندضلعی های متعامد دیگر به این بستگی ندارد که اضلاع حتماً یکدیگر را در زاویه قائمه ببینند بلکه اضلاع به طور طبیعی به دو مجموعه متناوب ( بخش های عمودی و افقی ) تقسیم می شوند.

wiki: چندضلعی ایزوتتیک
