در زمینه ریاضی تجزیه و تحلیل عددی ، چند جمله ای برنشتاین ، که به نام سرگئی ناتانوویچ برنشتاین نامگذاری شده است، چند جمله ای در فرم برنشتاین ترکیبی خطی از چند جمله ای های برنشتاین است .
روش عددی پایدار برای ارزیابی چند جمله ای ها به شکل برنشتاین به نام الگوریتم de Casteljau وجود دارد.
چند جمله ای های برنشتاین برای اولین بار توسط برنشتاین در اثبات سازنده قضیه تقریب Weierstrass استفاده شد. با ظهور گرافیک رایانه ای ، چند جمله های برنشتاین ، محدود به فاصله ، به شکل منحنی های بزیر شناخته شدند.
n + چند جمله ای های درجه 1 برنشتاین به عنوان n تعریف می شوند
جایی که ( n ν ) ضریب دوجمله ای است . به عنوان مثال ، b 2 , 5 ( x ) = ( 5 2 ) x 2 ( 1 − x ) 3 = 10 x 2 ( 1 − x ) 3 .
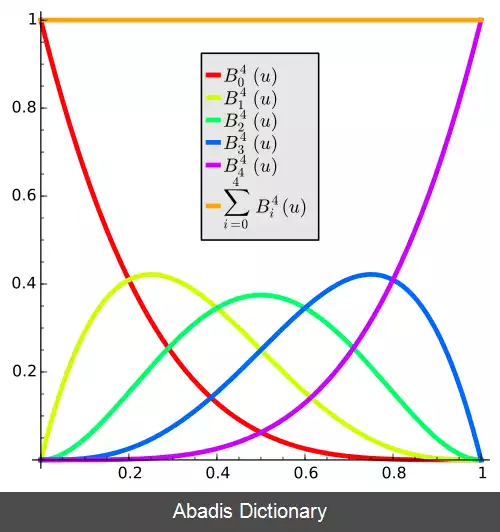
اولین چند جمله های اساسی برنشتاین برای ترکیب مقدارهای 1 ، 2 ، 3 یا 4 با هم عبارتند از:
چند جمله ای های پایه برنشتاین درجه n حداکثر مبنایی را برای فضای برداری P n از چند جمله ای های درجه n با ضرایب واقعی تشکیل می دهد. ترکیبی خطی از چند جمله ای مبتنی برنشتاین
در فرم درجه Bernnstein چند جمله ای یا چند جمله ای Bernstein از درجه n [ ۱] نامیده می شود. ضرایب β ν ضرایب برنشتاین یا ضرایب بزیر نامیده می شوند.
از اولین چند جمله ای های مبتنی برنشتاین در زیر آمده است که از بالا، دارای فقط یک جمله هستند:
چند جمله ای های برنشتاین دارای ویژگی های زیر است:
• b ν , n ( x ) = 0 {\displaystyle b_{\nu , n} ( x ) =0} ، اگر ν < 0 {\displaystyle \nu < 0} یا ν > n . {\displaystyle \nu > n. }
• b ν , n ( x ) ≥ 0 {\displaystyle b_{\nu , n} ( x ) \geq 0} برای x ∈ . {\displaystyle x\in . }
• b ν , n ( 1 − x ) = b n − ν , n ( x ) . {\displaystyle b_{\nu , n}\left ( 1 - x\right ) =b_{n - \nu , n} ( x ) . }
• b ν , n ( 0 ) = δ ν , 0 {\displaystyle b_{\nu , n} ( 0 ) =\delta _{\nu , 0}} و b ν , n ( 1 ) = δ ν , n {\displaystyle b_{\nu , n} ( 1 ) =\delta _{\nu , n}} جایی که δ {\displaystyle \delta } تابع دلتا Kronecker است: δ i j = { 0 if i ≠ j , 1 if i = j . {\displaystyle \delta _{ij}={\begin{cases}0& {\text{if }}i\neq j, \\1& {\text{if }}i=j. \end{cases}}}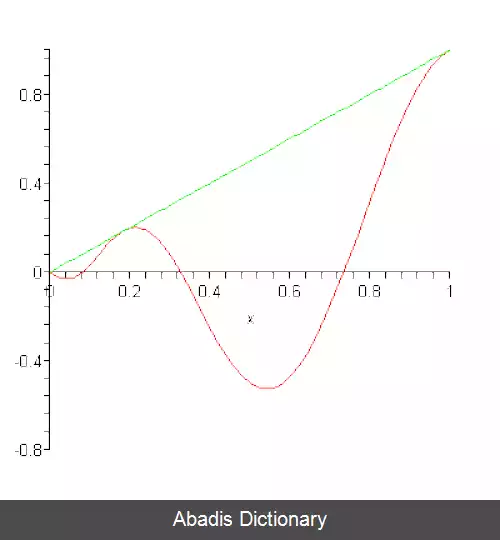
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفروش عددی پایدار برای ارزیابی چند جمله ای ها به شکل برنشتاین به نام الگوریتم de Casteljau وجود دارد.
چند جمله ای های برنشتاین برای اولین بار توسط برنشتاین در اثبات سازنده قضیه تقریب Weierstrass استفاده شد. با ظهور گرافیک رایانه ای ، چند جمله های برنشتاین ، محدود به فاصله ، به شکل منحنی های بزیر شناخته شدند.
n + چند جمله ای های درجه 1 برنشتاین به عنوان n تعریف می شوند
جایی که ( n ν ) ضریب دوجمله ای است . به عنوان مثال ، b 2 , 5 ( x ) = ( 5 2 ) x 2 ( 1 − x ) 3 = 10 x 2 ( 1 − x ) 3 .
اولین چند جمله های اساسی برنشتاین برای ترکیب مقدارهای 1 ، 2 ، 3 یا 4 با هم عبارتند از:
چند جمله ای های پایه برنشتاین درجه n حداکثر مبنایی را برای فضای برداری P n از چند جمله ای های درجه n با ضرایب واقعی تشکیل می دهد. ترکیبی خطی از چند جمله ای مبتنی برنشتاین
در فرم درجه Bernnstein چند جمله ای یا چند جمله ای Bernstein از درجه n [ ۱] نامیده می شود. ضرایب β ν ضرایب برنشتاین یا ضرایب بزیر نامیده می شوند.
از اولین چند جمله ای های مبتنی برنشتاین در زیر آمده است که از بالا، دارای فقط یک جمله هستند:
چند جمله ای های برنشتاین دارای ویژگی های زیر است:
• b ν , n ( x ) = 0 {\displaystyle b_{\nu , n} ( x ) =0} ، اگر ν < 0 {\displaystyle \nu < 0} یا ν > n . {\displaystyle \nu > n. }
• b ν , n ( x ) ≥ 0 {\displaystyle b_{\nu , n} ( x ) \geq 0} برای x ∈ . {\displaystyle x\in . }
• b ν , n ( 1 − x ) = b n − ν , n ( x ) . {\displaystyle b_{\nu , n}\left ( 1 - x\right ) =b_{n - \nu , n} ( x ) . }
• b ν , n ( 0 ) = δ ν , 0 {\displaystyle b_{\nu , n} ( 0 ) =\delta _{\nu , 0}} و b ν , n ( 1 ) = δ ν , n {\displaystyle b_{\nu , n} ( 1 ) =\delta _{\nu , n}} جایی که δ {\displaystyle \delta } تابع دلتا Kronecker است: δ i j = { 0 if i ≠ j , 1 if i = j . {\displaystyle \delta _{ij}={\begin{cases}0& {\text{if }}i\neq j, \\1& {\text{if }}i=j. \end{cases}}}


wiki: چندجمله ای های برنشتاین
