پیچیدگی نمونه یک الگوریتم یادگیری ماشین، برابر است با تعداد نمونه های یادگیری که برای موفقیت الگوریتم لازم است. به صورت دقیق تر، پیچیدگی نمونه برابر است با حداقل تعداد نمونه های لازم، تا تابع خروجی الگوریتم با احتمالی نزدیک به «یک» در فاصله ای نزدیک به «صفر» از تابع هدف قرار گیرد. پیچیدگی نمونه به دو صورت در نظر گرفته می شود:
• نوع ضعیف؛ که در آن فرضی روی توزیع احتمال ورودی و خروجی در نظر گرفته می شود.
• نوع قوی؛ که در آن فرضی روی توزیع احتمال ورودی و خروجی الگوریتم گذاشته نمی شود.
طبق قضیه از ناهار مجانی خبری نیست می دانیم که در حالت کلی، پیچیدگی نمونه نوع قوی بی نهایت است. به عبارت دیگر هیچ الگوریتم یادگیری ای وجود ندارد که بتواند با تعداد محدودی نمونه هر تابع هدفی را یاد بگیرد. به هرحال اگر خود را به توابع خاصی مانند توابع خطی یا توابع دودویی محدود کنیم؛ پیچیدگی نمونه محدود است و به بعد وی سی مربوط می شود. [ ۱]
اگر X را مجموعه ورودی های ممکن و Y را مجموعه خروجی های ممکن در نظر بگیریم، Z را به صورت ضرب دکارتی این دو مجموعه X × Y تعریف می کنیم. برای مثال برای مسئله دسته بندی دوکلاسه، X یک فضای برداری متناهی و Y برابر با مجموعه { 0 , 1 } است.
H را مجموعه ای از توابع h که h : X → Y است در نظر می گیریم. یک الگوریتم یادگیری A عبارت است از تابعی از Z ∗ به H . به عبارت دیگر یک الگوریتم یادگیری تعداد محدودی از نمونه های یادگیری را دریافت می کند و یک تابع h : X → Y را به عنوان خروجی برمی گرداند. یک تابع هزینه L : X × Y → R + را در نظر می گیریم، برای مثال این تابع می تواند تابع هزینه خطای مربعات L ( y , y ′ ) = ( y − y ′ ) 2 باشد. برای یک توزیع احتمال D داده شده روی X × Y متوسط خطای تابع h ، که یکی از اعضای کلاس فرضیه H است، به صورت زیر تعریف می شود.
E ( h ) := E D = ∫ X × Y L o s s ( h ( x ) , y ) d D ( x , y )
داده های آموزشی یک دنباله m تایی از زوج مرتب های ( x , y ) به صورت S m = ( ( x 1 , y 1 ) , . . . , ( x m , y m ) ) ∼ D m تشکیل می دهند، که تمامی آن ها به صورت یکسان و مستقل از توزیع D نمونه برداری شده اند. یک الگوریتم یادگیری A به هر دنباله از داده های آموزشی S m یکی از اعضای کلاس فرضیه H را نسبت می دهد. کمینه خطای کلاس فرضیه H به صورت زیر تعریف می شود.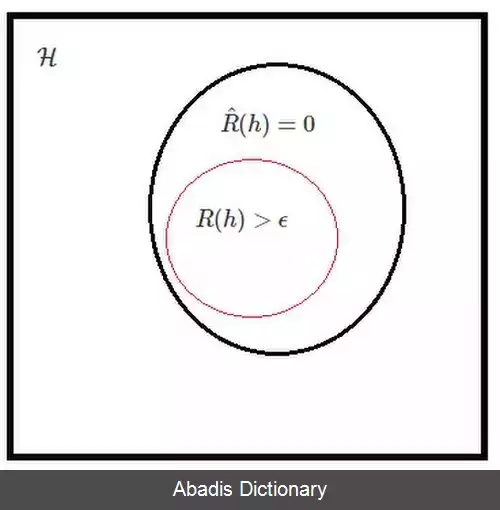
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• نوع ضعیف؛ که در آن فرضی روی توزیع احتمال ورودی و خروجی در نظر گرفته می شود.
• نوع قوی؛ که در آن فرضی روی توزیع احتمال ورودی و خروجی الگوریتم گذاشته نمی شود.
طبق قضیه از ناهار مجانی خبری نیست می دانیم که در حالت کلی، پیچیدگی نمونه نوع قوی بی نهایت است. به عبارت دیگر هیچ الگوریتم یادگیری ای وجود ندارد که بتواند با تعداد محدودی نمونه هر تابع هدفی را یاد بگیرد. به هرحال اگر خود را به توابع خاصی مانند توابع خطی یا توابع دودویی محدود کنیم؛ پیچیدگی نمونه محدود است و به بعد وی سی مربوط می شود. [ ۱]
اگر X را مجموعه ورودی های ممکن و Y را مجموعه خروجی های ممکن در نظر بگیریم، Z را به صورت ضرب دکارتی این دو مجموعه X × Y تعریف می کنیم. برای مثال برای مسئله دسته بندی دوکلاسه، X یک فضای برداری متناهی و Y برابر با مجموعه { 0 , 1 } است.
H را مجموعه ای از توابع h که h : X → Y است در نظر می گیریم. یک الگوریتم یادگیری A عبارت است از تابعی از Z ∗ به H . به عبارت دیگر یک الگوریتم یادگیری تعداد محدودی از نمونه های یادگیری را دریافت می کند و یک تابع h : X → Y را به عنوان خروجی برمی گرداند. یک تابع هزینه L : X × Y → R + را در نظر می گیریم، برای مثال این تابع می تواند تابع هزینه خطای مربعات L ( y , y ′ ) = ( y − y ′ ) 2 باشد. برای یک توزیع احتمال D داده شده روی X × Y متوسط خطای تابع h ، که یکی از اعضای کلاس فرضیه H است، به صورت زیر تعریف می شود.
E ( h ) := E D = ∫ X × Y L o s s ( h ( x ) , y ) d D ( x , y )
داده های آموزشی یک دنباله m تایی از زوج مرتب های ( x , y ) به صورت S m = ( ( x 1 , y 1 ) , . . . , ( x m , y m ) ) ∼ D m تشکیل می دهند، که تمامی آن ها به صورت یکسان و مستقل از توزیع D نمونه برداری شده اند. یک الگوریتم یادگیری A به هر دنباله از داده های آموزشی S m یکی از اعضای کلاس فرضیه H را نسبت می دهد. کمینه خطای کلاس فرضیه H به صورت زیر تعریف می شود.

wiki: پیچیدگی نمونه
