پیمایش گراهام روشی است برای محاسبه پوش محدب مجموعه متناهی از نقاط صفحه که پیچیدگی زمانی آن O ( n logn ) است. این الگوریتم به افتخار رونالد گراهام که نسخهٔ اصلی الگوریتم را در ۱۹۷۲ منتشر کرد نامگذاری شده است. این الگوریتم تمامی راس های مرزی پوش محدب به صورت مرتب می یابد.
اولین گام در این الگوریتم یافتن نقطه ای با کمترین y است. اگر چند نقطه با کمترین y وجود داشت، در این مجموعه نقطه با کمترین x انتخاب خواهد شد. این نقطه را P می نامیم. این مرحله به اندازه ( O ( n زمان می برد که n تعداد نقاط می باشد.
سپس مجموعه نقاط باید بر حسب افزایش زاویه ای که آن ها و نقطه P با محور X می سازند، مرتب شوند. از هر الگوریتم مرتب سازی برای این این مرحله می توان استفاده کرد به عنوان مثال مرتب سازی هرمی که پیچیدگی زمانی آن ( O ( n log n است.
برای افزایش سرعت محاسبه لازم نیست زاویهٔ واقعی که این نقاط با محور X می سازند محاسبه شود در عوض، محاسبه کسینوس این زاویه کافیست.
این الگوریتم با در نظر گرفتن هر نقطه در آرایه مرتب شده پیش می رود. برای هر نقطه این موضوع را در نظر می گیرد که آیا حرکت از دو نقطه ای که قبلاً در نظر گرفته به این نقطه یک چرخش به چب بوده یا چرخش به راست. اگر چرخش به راست باشد به این معناست که نقطه دوم به آخر بخشی از بدنه محدب نمی باشد و باید حذف شود. این فرایند تا زمانی ادامه می یابد که مجموعه سه نقطه آخر چرخش به راست باشد. به محض اینکه با یک چرخش به چپ مواجه شود الگوریتم به سراغ نقطه بعدی در آرایه مرتب شده می رود. ( اگر در هر مرحله سه نقطه در یک راستا باشند، ممکن است انتخاب شود یا دور انداخته شود چون در برخی برنامه ها لازم است همه نقاط روی مرز بدنه محدب پیدا شوند.
بازهم برای تعیین اینکه آیا سه نقطه تشکیل یک چرخش به چپ را می دهند یا چرخش به راست، نیازی نیست زاویه واقعی میان دو پاره خط محاسبه شود و در واقع می توانید تنها با حسابی ساده به این هدف برسید. برای سه نقطه ( x1, y1 ) ، ( x2, y2 ) و ( x3, y3 ) ، محاسبه جهت ضرب خارجی دو برداری که با نقاط ( x1, y1 ) , ( x2, y2 ) و ( x1, y1 ) , ( x3, y3 ) تعریف می شوداز طریق تعیین علامت عبارت ( x2 − x1 ) ( y3 − y1 ) − ( y2 − y1 ) ( x3 − x1 ) میسر است. اگر این عبارت صفر شد نقاط هم راستا هستند. اگر مثبت شد نقاط یک گردش به چپ و در غیر اینصورت یک گردش به راست را تشکیل می دهند.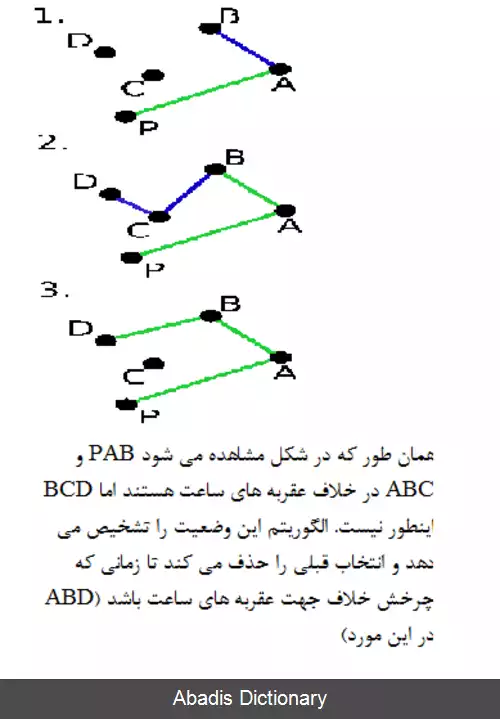
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاولین گام در این الگوریتم یافتن نقطه ای با کمترین y است. اگر چند نقطه با کمترین y وجود داشت، در این مجموعه نقطه با کمترین x انتخاب خواهد شد. این نقطه را P می نامیم. این مرحله به اندازه ( O ( n زمان می برد که n تعداد نقاط می باشد.
سپس مجموعه نقاط باید بر حسب افزایش زاویه ای که آن ها و نقطه P با محور X می سازند، مرتب شوند. از هر الگوریتم مرتب سازی برای این این مرحله می توان استفاده کرد به عنوان مثال مرتب سازی هرمی که پیچیدگی زمانی آن ( O ( n log n است.
برای افزایش سرعت محاسبه لازم نیست زاویهٔ واقعی که این نقاط با محور X می سازند محاسبه شود در عوض، محاسبه کسینوس این زاویه کافیست.
این الگوریتم با در نظر گرفتن هر نقطه در آرایه مرتب شده پیش می رود. برای هر نقطه این موضوع را در نظر می گیرد که آیا حرکت از دو نقطه ای که قبلاً در نظر گرفته به این نقطه یک چرخش به چب بوده یا چرخش به راست. اگر چرخش به راست باشد به این معناست که نقطه دوم به آخر بخشی از بدنه محدب نمی باشد و باید حذف شود. این فرایند تا زمانی ادامه می یابد که مجموعه سه نقطه آخر چرخش به راست باشد. به محض اینکه با یک چرخش به چپ مواجه شود الگوریتم به سراغ نقطه بعدی در آرایه مرتب شده می رود. ( اگر در هر مرحله سه نقطه در یک راستا باشند، ممکن است انتخاب شود یا دور انداخته شود چون در برخی برنامه ها لازم است همه نقاط روی مرز بدنه محدب پیدا شوند.
بازهم برای تعیین اینکه آیا سه نقطه تشکیل یک چرخش به چپ را می دهند یا چرخش به راست، نیازی نیست زاویه واقعی میان دو پاره خط محاسبه شود و در واقع می توانید تنها با حسابی ساده به این هدف برسید. برای سه نقطه ( x1, y1 ) ، ( x2, y2 ) و ( x3, y3 ) ، محاسبه جهت ضرب خارجی دو برداری که با نقاط ( x1, y1 ) , ( x2, y2 ) و ( x1, y1 ) , ( x3, y3 ) تعریف می شوداز طریق تعیین علامت عبارت ( x2 − x1 ) ( y3 − y1 ) − ( y2 − y1 ) ( x3 − x1 ) میسر است. اگر این عبارت صفر شد نقاط هم راستا هستند. اگر مثبت شد نقاط یک گردش به چپ و در غیر اینصورت یک گردش به راست را تشکیل می دهند.

wiki: پیمایش گراهام
