در علم کامپیوتر پیمایش درخت شکلی از پیمایش گراف است و به پروسه ملاقات گره ها در ساختمان دادهٔ درخت اشاره دارد، به نحوی سیسیبهر گره دقیقاً یک بار ملاقات شود. این گونه پیمایش ها به ترتیب گره ای که ملاقات می کنند دسته بندی شده اند. الگوریتم های زیر برای یک درخت دودویی شرح داده شده اند اما ممکن است قابل تعمیم به سایر درخت ها نیز باشند.
در مقایسه با ساختمان داده های خطی مانند لیست های پیوندی و آرایه یک بعدی که یک روش پیمایش استاندارد دارند؛ ساختارهای درختی می توانند در مسیرهای مختلفی پیمایش شوند. برای شروع از ریشه یک درخت دودویی سه گام اصلی وجود دارد که ترتیب انجام آن ها نوع پیمایش درختی را مشخص می کند. این مراحل عبارتند از: انجام یک عمل در گره فعلی که اشاره به دیدن گره دارد، پیمایش به سمت گره فرزند چپ و پیمایش به سمت گره فرزند راست در برخی از روش ها پیمایش شامل تکرار همه گره ها می شود. چراکه از گره داده شده ممکن است بیش از یک گره بعدی وجود داشته باشد ( در این حالت آن ساختمان داده خطی نیست ) پس با فرض محاسبهٔ متوالی ( نه موازی ) بعضی از گره ها باید در برخی مسیرها به تعویق بیفتند و برای ملاقات های بعدی ذخیره شوند. این کار اغلب بواسطه پشته و از طریق الگوریتم LIFO یا از طریق صف و از طریق الگوریتم FIFO انجام می شود. ساختمان داده همانند یک درخت بازگشتی است، پیمایش می تواند به عنوان یک بازگشت تعریف شود، در یک مد طبیعی و روشن گره های معوق به صورت ضمنی در پشته تماس ذخیره می شوند. نامی که به پیمایش ها داده می شود از ترتیبی که آن ها گره ها را ملاقات می کنند گرفته شده است. به بیان ساده تر پیشروی به سمت پایین ( اول - عمق، فرزند اول سپس نوه، قبل از فرزند دوم ) یا اول - سطح ( اول سطح یا عرض، فرزند اول سپس فرزند دوم قبل از نوه ) پیمایش های اول –عمق بیشتر بر اساس وضعیت عناصر ریشه با توجه به گره های موجود در سمت چپ و راست دسته بندی شده اند. تصور کنید که گره چپ و راست در مکان خود ثابت هستند، پس گره ریشه می تواند در طرف چپ گره سمت چپ قرار داده شود ( پیمایش پیشوندی ) یا اینکه بین گره راست و چپ قرار گیرد ( پیمایش میانوندی ) یا طرف راست گره سمت راست باشد ( پیمایش پسوندی ) . هیچگونه اختلاف مشابهی در پیمایش اول - سطح که به گره فرزند نسبت داده شده وجود ندارد؛ در نتیجه پیمایش اول - سطح بی ابهام و واضح است. برای طراحی همیشه فرض بر این است که گره های سمت چپ بر گره های سمت راست مقدم هستند. این مرتب سازی می تواند تا زمانی که همین ترتیب برای همه روش های پیمایش، درنظرگرفته وارونه شود. پیمایش اول عمق از طریق پشته به آسانی قابل پیاده سازی است، در حالی که اول سطح به سادگی از طریق صف قابل پیاده سازی است. فراتر از این پیمایش ها عمومی طرح های پیچیده تر و ترکیبی مختلفی نیز قابل پیاده سازی است، نظیر جستجوهای عمق محدود ( depth - limited ) ، جستجوی تعمیق تکراری ( iterative deepening depth - first ) . می خواهیم با حرکت روی یال های یک درخت، همهٔ گره های آن را هر کدام یک بار ملاقات کنیم. به این کار پیمایش درخت می گویند. بسته به این که کدام عنصر، کی ملاقات شود، پیمایش درخت لیست یا یک ترتیب خطی از عناصر آن درخت به ما می دهد. طبیعتاً پیمایش های متفاوت ترتیب های متفاوتی خواهند داد. دو روش عمقل اول و سطح اول، دو روش معمول پیمایش درخت هستند که بیشتر برای پیمایش درخت دودویی به کار می روند.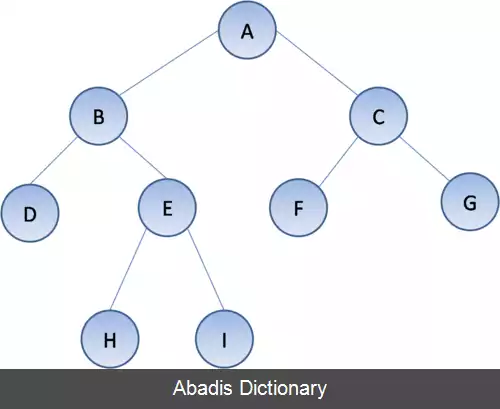
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر مقایسه با ساختمان داده های خطی مانند لیست های پیوندی و آرایه یک بعدی که یک روش پیمایش استاندارد دارند؛ ساختارهای درختی می توانند در مسیرهای مختلفی پیمایش شوند. برای شروع از ریشه یک درخت دودویی سه گام اصلی وجود دارد که ترتیب انجام آن ها نوع پیمایش درختی را مشخص می کند. این مراحل عبارتند از: انجام یک عمل در گره فعلی که اشاره به دیدن گره دارد، پیمایش به سمت گره فرزند چپ و پیمایش به سمت گره فرزند راست در برخی از روش ها پیمایش شامل تکرار همه گره ها می شود. چراکه از گره داده شده ممکن است بیش از یک گره بعدی وجود داشته باشد ( در این حالت آن ساختمان داده خطی نیست ) پس با فرض محاسبهٔ متوالی ( نه موازی ) بعضی از گره ها باید در برخی مسیرها به تعویق بیفتند و برای ملاقات های بعدی ذخیره شوند. این کار اغلب بواسطه پشته و از طریق الگوریتم LIFO یا از طریق صف و از طریق الگوریتم FIFO انجام می شود. ساختمان داده همانند یک درخت بازگشتی است، پیمایش می تواند به عنوان یک بازگشت تعریف شود، در یک مد طبیعی و روشن گره های معوق به صورت ضمنی در پشته تماس ذخیره می شوند. نامی که به پیمایش ها داده می شود از ترتیبی که آن ها گره ها را ملاقات می کنند گرفته شده است. به بیان ساده تر پیشروی به سمت پایین ( اول - عمق، فرزند اول سپس نوه، قبل از فرزند دوم ) یا اول - سطح ( اول سطح یا عرض، فرزند اول سپس فرزند دوم قبل از نوه ) پیمایش های اول –عمق بیشتر بر اساس وضعیت عناصر ریشه با توجه به گره های موجود در سمت چپ و راست دسته بندی شده اند. تصور کنید که گره چپ و راست در مکان خود ثابت هستند، پس گره ریشه می تواند در طرف چپ گره سمت چپ قرار داده شود ( پیمایش پیشوندی ) یا اینکه بین گره راست و چپ قرار گیرد ( پیمایش میانوندی ) یا طرف راست گره سمت راست باشد ( پیمایش پسوندی ) . هیچگونه اختلاف مشابهی در پیمایش اول - سطح که به گره فرزند نسبت داده شده وجود ندارد؛ در نتیجه پیمایش اول - سطح بی ابهام و واضح است. برای طراحی همیشه فرض بر این است که گره های سمت چپ بر گره های سمت راست مقدم هستند. این مرتب سازی می تواند تا زمانی که همین ترتیب برای همه روش های پیمایش، درنظرگرفته وارونه شود. پیمایش اول عمق از طریق پشته به آسانی قابل پیاده سازی است، در حالی که اول سطح به سادگی از طریق صف قابل پیاده سازی است. فراتر از این پیمایش ها عمومی طرح های پیچیده تر و ترکیبی مختلفی نیز قابل پیاده سازی است، نظیر جستجوهای عمق محدود ( depth - limited ) ، جستجوی تعمیق تکراری ( iterative deepening depth - first ) . می خواهیم با حرکت روی یال های یک درخت، همهٔ گره های آن را هر کدام یک بار ملاقات کنیم. به این کار پیمایش درخت می گویند. بسته به این که کدام عنصر، کی ملاقات شود، پیمایش درخت لیست یا یک ترتیب خطی از عناصر آن درخت به ما می دهد. طبیعتاً پیمایش های متفاوت ترتیب های متفاوتی خواهند داد. دو روش عمقل اول و سطح اول، دو روش معمول پیمایش درخت هستند که بیشتر برای پیمایش درخت دودویی به کار می روند.

wiki: پیمایش درخت
