پویایی شناسی سامانه ها یا دینامیک سامانه ها ( به انگلیسی: System dynamics ) ، روشی برای درک رفتارهای یک سامانهٔ پیچیده در طول زمان است. در این روش با تمرکز بر حلقه های بازخورد ( Feedback Loops ) درون سامانه، تأثیرات غیرخطی و تاخیرهای زمانی در میان متغیرها و همچنین ماهیت انباشتی یا جریانی متغیرها به بررسی رفتار یک سامانه می پردازند. با توجه به ماهیت عددی روش پویایی های سامانه، این امکان وجود دارد که مدل های مبتنی بر این روش را با استفاده بهینه از رایانه شبیه سازی کرد و با مجموعه پارامترها و متغیرهای مختلف وضعیت سامانه برای یک بازه زمانی در آینده را پیش بینی نمود.
پویایی های سامانه با حلقه های بازخورد و تأخیرهای زمانی سروکار دارد که رفتار کل سامانه را مورد تأثیر قرار می دهند. چیزی که استفاده از پویایی های سامانه را از دیگر رویکردهای مطالعهٔ سامانه های پیچیده متمایز می سازد استفاده از حلقه های بازخورد و انباشت و جریان است. این عناصر به شرح چگونگی نمایش تأثیرات غیر خطی در سامانه های بظاهر ساده کمک می کنند.
پویایی های سامانه یک روش شناسی و روش مدل سازی ریاضی برای چارچوب بندی، درک، و بحث پیرامون موضوعات و مسائل پیچیده است. در حالیکه در دههٔ ۱۹۵۰ برای کمک به مدیران شرکت ها بمنظور بهبود درکشان از فرایندهای صنعتی ایجاد شد، در حال حاضر پویایی های سامانه در تمام بخش عمومی و خصوصی بمنظور طراحی و آنالیز سیاست ها بکار می رود.
در دههٔ ۱۹۹۰ نرم افزار مناسب پویایی های سامانه در نسخه های کاربرپسند توسعه یافت و به سامانه های گوناگون اعمال شد. مدل های پویایی های سامانه، مشکل همزمانی ( علت و معلول متقابل ) را با بروزرسانی کلیهٔ متغیرها در افزایش های زمانی کوچک با بازخوردهای مثبت و منفی و تأخیرهای زمانی برای ساختاربندی تعاملات و کنترل، حل می کنند. احتمالاً بهترین مدل شناخته شدهٔ پویایی های سامانه مربوط به کتاب «محدودیت های رشد»[ ۱] چاپ ۱۹۷۲ باشد. این مدل پیش بینی می کند که رشد تصاعدی منجر به فروپاشی اقتصادی در سدهٔ ۲۱ میلادی تحت طیف گسترده ای از سناریوهای رشد شود.
پویایی های سامانه جنبه ای از نظریهٔ سامانه ها به عنوان روشی برای درک رفتار پویای سامانه های پیچیده است. اساس روش، درک این مسئله است که ساختار هر سامانه — با روابط دایره ای، به هم پیوسته، و گاهی با تأخیر زمانی بین اجزایشان — اغلب به همان اندازه ای در تعیین رفتار اهمیت دارد که خود اجزاء به صورت منفرد. مثال هایش نظریه آشوب و پویایی اجتماعی است. همچنین ادعا شده که اغلب به دلیل وجود خواص کلی ای که نمی توان آن ها را در خواص اجزاء یافت، در برخی موارد نمی توان به توضیح رفتار کل در قالب رفتار اجزاء پرداخت.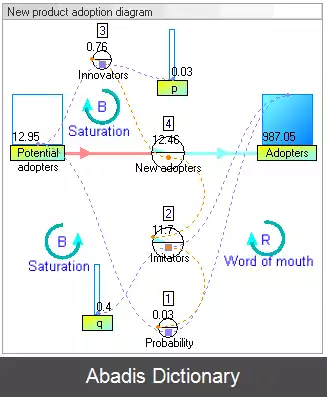

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفپویایی های سامانه با حلقه های بازخورد و تأخیرهای زمانی سروکار دارد که رفتار کل سامانه را مورد تأثیر قرار می دهند. چیزی که استفاده از پویایی های سامانه را از دیگر رویکردهای مطالعهٔ سامانه های پیچیده متمایز می سازد استفاده از حلقه های بازخورد و انباشت و جریان است. این عناصر به شرح چگونگی نمایش تأثیرات غیر خطی در سامانه های بظاهر ساده کمک می کنند.
پویایی های سامانه یک روش شناسی و روش مدل سازی ریاضی برای چارچوب بندی، درک، و بحث پیرامون موضوعات و مسائل پیچیده است. در حالیکه در دههٔ ۱۹۵۰ برای کمک به مدیران شرکت ها بمنظور بهبود درکشان از فرایندهای صنعتی ایجاد شد، در حال حاضر پویایی های سامانه در تمام بخش عمومی و خصوصی بمنظور طراحی و آنالیز سیاست ها بکار می رود.
در دههٔ ۱۹۹۰ نرم افزار مناسب پویایی های سامانه در نسخه های کاربرپسند توسعه یافت و به سامانه های گوناگون اعمال شد. مدل های پویایی های سامانه، مشکل همزمانی ( علت و معلول متقابل ) را با بروزرسانی کلیهٔ متغیرها در افزایش های زمانی کوچک با بازخوردهای مثبت و منفی و تأخیرهای زمانی برای ساختاربندی تعاملات و کنترل، حل می کنند. احتمالاً بهترین مدل شناخته شدهٔ پویایی های سامانه مربوط به کتاب «محدودیت های رشد»[ ۱] چاپ ۱۹۷۲ باشد. این مدل پیش بینی می کند که رشد تصاعدی منجر به فروپاشی اقتصادی در سدهٔ ۲۱ میلادی تحت طیف گسترده ای از سناریوهای رشد شود.
پویایی های سامانه جنبه ای از نظریهٔ سامانه ها به عنوان روشی برای درک رفتار پویای سامانه های پیچیده است. اساس روش، درک این مسئله است که ساختار هر سامانه — با روابط دایره ای، به هم پیوسته، و گاهی با تأخیر زمانی بین اجزایشان — اغلب به همان اندازه ای در تعیین رفتار اهمیت دارد که خود اجزاء به صورت منفرد. مثال هایش نظریه آشوب و پویایی اجتماعی است. همچنین ادعا شده که اغلب به دلیل وجود خواص کلی ای که نمی توان آن ها را در خواص اجزاء یافت، در برخی موارد نمی توان به توضیح رفتار کل در قالب رفتار اجزاء پرداخت.






wiki: پویایی شناسی سیستم ها
