در نظریه گراف ، پوشش راسی ( پوشش گره ای ) در یک گراف ، زیرمجموعه ای از رئوس است که که همهٔ یال های این گراف را می پوشاند. در این جا پوشش یک یال یعنی آن که دست کم یکی از گره های دو سر یال در این زیرمجموعه باشد. اندازهٔ پوششی گره ای برابر است با شمار گره های درون این مجموعه. برای نمونه، شکل زیر دارای یک پوشش گره ای ، به اندازهٔ ۲ است.
پرسمان یافتن پوشش گره ای کمینه به یافتن پوششی گره ای می پردازد که کم ترین شمار گره ها را دربرداشته باشد. این پرسمان ان پی کامل است، از این روی رایانش چنین زیرمجموعه ای دشوار است . این مسئله در علوم کامپیوتر ، یک مسئله بهینه سازی کلاسیک است. پس این پرسمان NP - سخت است درنتیجه اگر P ≠ NP باشد، نمی توان آن را با یک الگوریتم زمان چند جمله ای حل کرد. علاوه بر این، تخمین زدن آن دشوار است - اگر حدس بازی های منحصر به فرد درست باشد، نمی توان آن را تا ضریب کوچکتر از 2 تقریب زد.
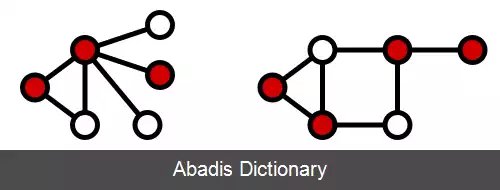
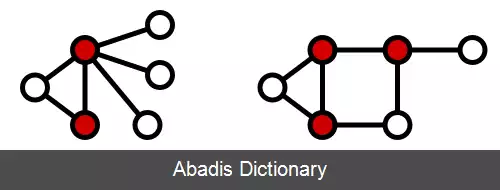
برای گرافی بی سو مانند G = ( V , E ) ، زیرمجموعه ای V ′ ⊆ V پوشش گره ای است اگر برای هر یال ( u , v ) ∈ E یا گره v ∈ V ′ یا گرهٔ u ∈ V ′ یا { u , v } ⊆ V ′ باشد. دو پوشش گره ای با رنگ قرمز در شکل های زیر نمایانیده شده اند.
اندازهٔ پوششی گره ای مانند V ′ برابر است با شمار گره های این زیرمجموعه که با | V ′ | نمایش داده می شود. پوشش گره ای کمینه پوششی است که دارای کم ترین گره ها باشد. گره های سرخ در در دو شکل زیر پوشش گره ای کمینه را برای نمونه های بالا می نمایانند.
• مجموعهٔ همهٔ گره ها پوشش گره ای است.
• گره های تطابق ( گراف ) بیشینه ای یک پوشش گره ای را می سازند.
• گراف دوبخشی کامل K m , n {\displaystyle K_{m, n}} دارای پوششی گره ای کمینه با اندازه min ( m , n ) {\displaystyle \min ( m, n ) } است.
• مجموعه ای از گره ها پوششی گره ای است اگر و تنها اگر اُسپُران ( مکمل ) آن مجموعه ناوابسته باشد.
• شمار گره های گرافی برابر است با اندازهٔ پوشش گره ای کمینه و اندازهٔ مجموعهٔ ناوابسته بیشینهٔ این گراف ( Gallai ) .
پرسمان پوشش گره ای کمینه پرسمانی بهینه سازی است که به یافتن پوششی گره با کمترین اندازه برای یک گراف می پردازد. اگر گره ها وزن دار باشند، پوشش گره ای وزن دار کمینه زیرمجموعه ای از گره هاست که کمترین وزن را روی - هم - رفته داشته باشند.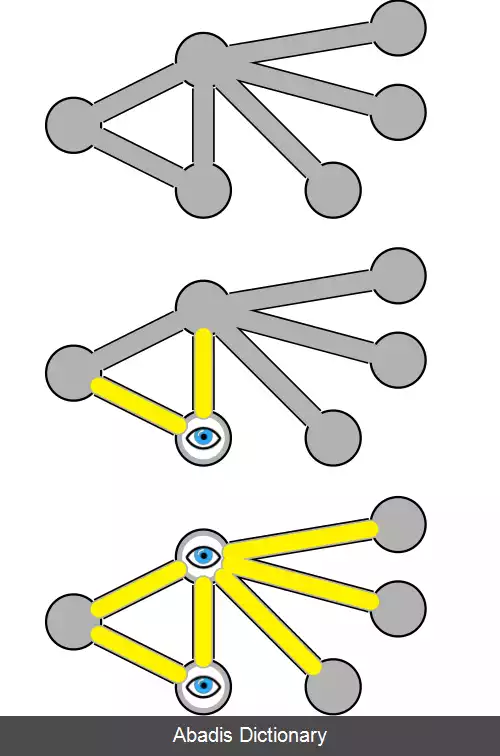
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفپرسمان یافتن پوشش گره ای کمینه به یافتن پوششی گره ای می پردازد که کم ترین شمار گره ها را دربرداشته باشد. این پرسمان ان پی کامل است، از این روی رایانش چنین زیرمجموعه ای دشوار است . این مسئله در علوم کامپیوتر ، یک مسئله بهینه سازی کلاسیک است. پس این پرسمان NP - سخت است درنتیجه اگر P ≠ NP باشد، نمی توان آن را با یک الگوریتم زمان چند جمله ای حل کرد. علاوه بر این، تخمین زدن آن دشوار است - اگر حدس بازی های منحصر به فرد درست باشد، نمی توان آن را تا ضریب کوچکتر از 2 تقریب زد.
برای گرافی بی سو مانند G = ( V , E ) ، زیرمجموعه ای V ′ ⊆ V پوشش گره ای است اگر برای هر یال ( u , v ) ∈ E یا گره v ∈ V ′ یا گرهٔ u ∈ V ′ یا { u , v } ⊆ V ′ باشد. دو پوشش گره ای با رنگ قرمز در شکل های زیر نمایانیده شده اند.
اندازهٔ پوششی گره ای مانند V ′ برابر است با شمار گره های این زیرمجموعه که با | V ′ | نمایش داده می شود. پوشش گره ای کمینه پوششی است که دارای کم ترین گره ها باشد. گره های سرخ در در دو شکل زیر پوشش گره ای کمینه را برای نمونه های بالا می نمایانند.
• مجموعهٔ همهٔ گره ها پوشش گره ای است.
• گره های تطابق ( گراف ) بیشینه ای یک پوشش گره ای را می سازند.
• گراف دوبخشی کامل K m , n {\displaystyle K_{m, n}} دارای پوششی گره ای کمینه با اندازه min ( m , n ) {\displaystyle \min ( m, n ) } است.
• مجموعه ای از گره ها پوششی گره ای است اگر و تنها اگر اُسپُران ( مکمل ) آن مجموعه ناوابسته باشد.
• شمار گره های گرافی برابر است با اندازهٔ پوشش گره ای کمینه و اندازهٔ مجموعهٔ ناوابسته بیشینهٔ این گراف ( Gallai ) .
پرسمان پوشش گره ای کمینه پرسمانی بهینه سازی است که به یافتن پوششی گره با کمترین اندازه برای یک گراف می پردازد. اگر گره ها وزن دار باشند، پوشش گره ای وزن دار کمینه زیرمجموعه ای از گره هاست که کمترین وزن را روی - هم - رفته داشته باشند.




wiki: پوشش گرهی
