در تئوری گراف، یک تجزیهٔ مسیر در گراف G، به طور غیر رسمی، نمایش G به صورت مسیرهای به هم چسبیده است و پهنای مسیر G، یک عدد است که مقدار ضخیم شدن مسیر برای شکل دادن گراف را اندازه می گیرد. به عبارت دیگر تجزیهٔ مسیر، دنباله ای از زیرمجموعه های رئوس گراف است به طوری که رئوس سر یالهای G در یکی از زیرمجموعه ها ظاهر می شود به طوری که هر رأس در زیردنبالهٔ متوالی از زیرمجموعه ها ظاهر می شود و پهنای مسیر اندازهٔ بزرگترین مجموعه در یک تجزیهٔ مسیر منهای یک است. به پهنای مسیر ضخامت بازه ( یکی کمتر از اندازهٔ ماکزیمم کلیک دربازه سوپرگراف G ) ، عدد جداکنندهٔ رئوس و عدد جستجوکنندهٔ گره هم می گویند.
پهنای مسیر و تجزیهٔ مسیر خیلی شبیه پهنای درخت و تجزیهٔ درخت است. آن ها نقش کلیدی در تئوری مینورهای گراف: خانواده ای از گراف ها که تحت مینورهای گراف بسته اند و دارای کل جنگل ها نمی باشد ممکن است توصیف گردد به گراف هایی با پهنای مسیر محدود و رئوس در ساختار تئوری برای گراف هایی که تحت مینور بسته اند دارای پهنای مسیر محدود هستند. پهنای مسیر و گراف های با پهنای مسیر محدود دارای برنامه های کاربردی در طراحیVLSI، طراحی گراف و زبان شناسی رایانشی است. پیدا کردن پهنای مسیر در گراف مسئلهٔ NP - hard است. به هر حال مسئله پارامتر - ثابت اداره پذیر ( Fixed - parameter tractability ) است: چک کردن اینکه گراف دارای پهنای مسیر به اندازهٔ k است، قابل حل در زمان نمایی است ولی برای درخت ها مستقل از k در زمان چندجمله ای قابل حل است. بسیاری از مسائل در الگوریتم های گرافهای با پهنای مسیر محدود، با برنامه نویسی پویا روی تجزیهٔ مسیر گراف، به طور مؤثر قابل حل است. تجزیهٔ مسیر ممکن است در اندازه گیری مقدار زمان اجرای الگوریتم در برنامه نویسی پویا روی گراف های با پهنای درخت محدود قابل استفاده باشد.
در مقالات معروفی مانند graph minors، Neil Robertson و ( Paul Seymour ( 1983 تجزیهٔ مسیر در گراف G را دنباله ای از زیرمجموعه های Xi از رئوس G، با دو ویژگی زیر:
• برای هر یال G، i ای وجود دارد که دو رأس سر یال در زیرمجموعهٔ Xi وجود دارد.
• برای هر سه اندیس i ≤ j ≤ k , Xi ∩ Xk ⊆ Xj
دومین ویژگی مستلزم می سازد که زیرمجموعه ها، زیردنباله متوالی از کل دنباله را بسازد. به زبان آخرین مقاله هایRobertson و Seymour تجزیهٔ مسیر یک تجزیهٔ درخت ( X, T ) است که درخت T از تجزیه یک مسیر گراف است. پهنای مسیر در تجزیهٔ مسیر مانند تجزیهٔ درخت تعریف می گردد ( 1 - |maxi |Xi ) و پهنای مسیر گراف G، مینیمم پهنای هر مسیر در تجزیهٔ مسیر است. یکی کم کردن از |Xi|تأثیر کمی در بیشتر برنامه ها می گذارد اما تعریف پهنای مسیر در گراف آن است.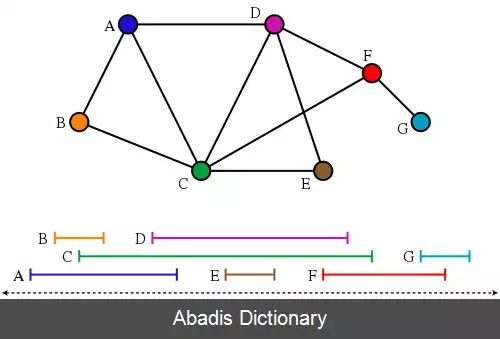
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفپهنای مسیر و تجزیهٔ مسیر خیلی شبیه پهنای درخت و تجزیهٔ درخت است. آن ها نقش کلیدی در تئوری مینورهای گراف: خانواده ای از گراف ها که تحت مینورهای گراف بسته اند و دارای کل جنگل ها نمی باشد ممکن است توصیف گردد به گراف هایی با پهنای مسیر محدود و رئوس در ساختار تئوری برای گراف هایی که تحت مینور بسته اند دارای پهنای مسیر محدود هستند. پهنای مسیر و گراف های با پهنای مسیر محدود دارای برنامه های کاربردی در طراحیVLSI، طراحی گراف و زبان شناسی رایانشی است. پیدا کردن پهنای مسیر در گراف مسئلهٔ NP - hard است. به هر حال مسئله پارامتر - ثابت اداره پذیر ( Fixed - parameter tractability ) است: چک کردن اینکه گراف دارای پهنای مسیر به اندازهٔ k است، قابل حل در زمان نمایی است ولی برای درخت ها مستقل از k در زمان چندجمله ای قابل حل است. بسیاری از مسائل در الگوریتم های گرافهای با پهنای مسیر محدود، با برنامه نویسی پویا روی تجزیهٔ مسیر گراف، به طور مؤثر قابل حل است. تجزیهٔ مسیر ممکن است در اندازه گیری مقدار زمان اجرای الگوریتم در برنامه نویسی پویا روی گراف های با پهنای درخت محدود قابل استفاده باشد.
در مقالات معروفی مانند graph minors، Neil Robertson و ( Paul Seymour ( 1983 تجزیهٔ مسیر در گراف G را دنباله ای از زیرمجموعه های Xi از رئوس G، با دو ویژگی زیر:
• برای هر یال G، i ای وجود دارد که دو رأس سر یال در زیرمجموعهٔ Xi وجود دارد.
• برای هر سه اندیس i ≤ j ≤ k , Xi ∩ Xk ⊆ Xj
دومین ویژگی مستلزم می سازد که زیرمجموعه ها، زیردنباله متوالی از کل دنباله را بسازد. به زبان آخرین مقاله هایRobertson و Seymour تجزیهٔ مسیر یک تجزیهٔ درخت ( X, T ) است که درخت T از تجزیه یک مسیر گراف است. پهنای مسیر در تجزیهٔ مسیر مانند تجزیهٔ درخت تعریف می گردد ( 1 - |maxi |Xi ) و پهنای مسیر گراف G، مینیمم پهنای هر مسیر در تجزیهٔ مسیر است. یکی کم کردن از |Xi|تأثیر کمی در بیشتر برنامه ها می گذارد اما تعریف پهنای مسیر در گراف آن است.


wiki: پهنای مسیر
