پس پرش (الگوریتم). در الگوریتمهای پس گرد ( backtrack ) روشی به نام پَس پَرش ( backjumping ) وجود دارد که باعث کاهش فضای جستجو، در نتیجه افزایش بهره وری است. در پس گرد همواره یک سطح در درخت جستجو بالا می رویم زمانی که تمامی مقادیر گره ها بررسی شده باشند، اما در روش پس پرش ممکن است چندین سطح به بالا پرش انجام دهیم. در این مقاله، مقادیر امتحانی ثابتی در نظر گرفته ایم x1 , x2 , … , xn که ممکن است به صورت غیر مرتّب نیز از آن ها استفاده نماییم.
در روش پس گرد زمانی که مقادیر یک متغیّر مورد بررسی قرار بگیرد و جستجو بی نتیجه پایان یابد، الگوریتم مقدار آخرین متغیرهای گره پیشین مورد بررسی قرار می دهد ولی اگر به انتها رسید و تمامی گره ها بررسی شد و به جواب درستی نرسیدیم، مقدار گره جستجو را تغییر و عملیات جستجو دوباره تکرار می شود. اگر شرایط به این گونه باشد x1=a1, …، xk =ak و تمامی مقادیر برای xk+1 بدون نتیجه برای پیدا کردن راه کار به پایان برسد الگوریتم یک سطح به بالا یعنی گره xk می رود؛ و در صورت امکان، مقدار را عوض کرده و به بالا بازمی گردد و سپس دوباره این مراحل را تکرار می کند.
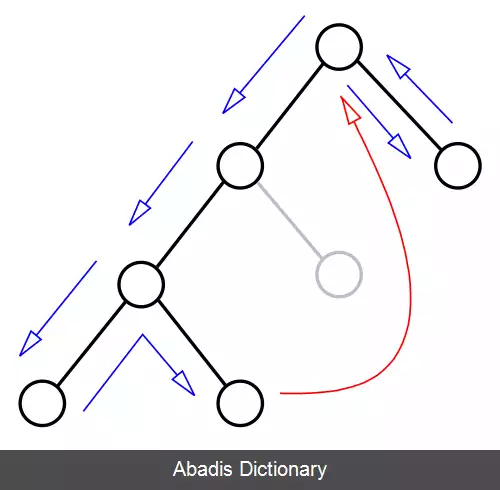
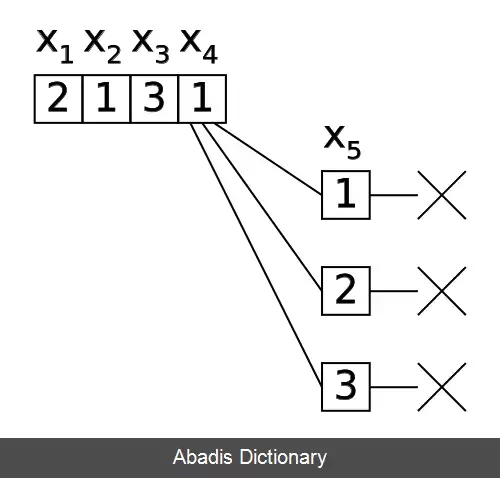
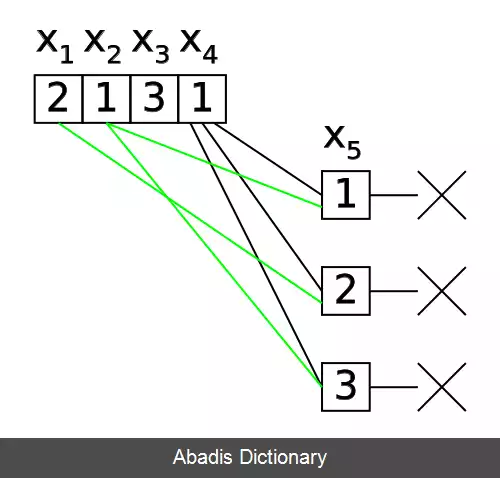
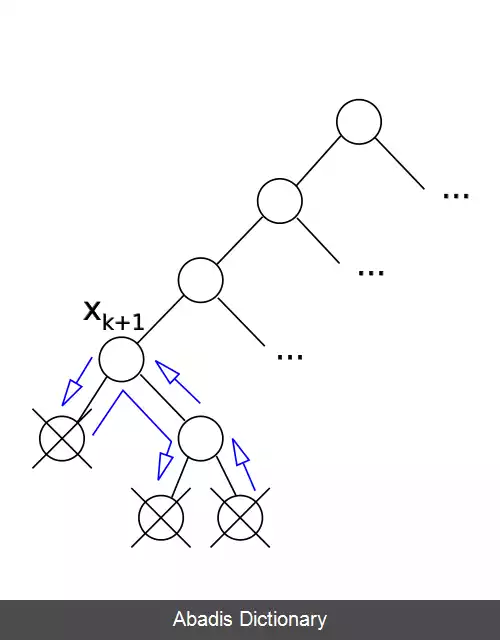
انتخاب مقدار تخصیص جزئی xk+1 همواره به صورت کامل برای پیدا کردن راه حل ضروری نیست چرا که اجباراً ما را به سمت جواب پایانی هدایت نمی کند. اگر شرایط به این گونه باشد x1=a1, …xk=ak و تمامی مقادیر برای xk+1 بدون نتیجه برای پیدا کردن راه کار به پایان برسد الگوریتم یک سطح به بالا یعنی گره xk رفته و در صورت امکان مقدار را عوض کرده سپس دوباره این مراحل را تکرار می کند. انتخاب مقدار تخصیص جزئی xk+1 همواره به صورت کامل برای پیدا کردن راه حل ضروری نیست اما یک پیشوند تخصیص جزئی ممکن است در حل مسائل ارزش زیادی داشته باشد. برای این منظور از ایندکسهایی با شرط j < k استفاده می کنیم همانند x1, …، xj=a1, …، aj. این کار زمانی اتفاق می افتد که قابل بسط بیشتر برای ساختن یک راه حل برای xk+1 نیستیم. اگر الگوریتم بتواند اثبات کند این نکته را، می تواند به صورت مستقیم یک گره جدیدی برای xj به جای xk جدید انتخاب نماید.
میزان بهره وری الگوریتم پس پرش میزان پرش به عقبی است که می تواند اتفاق بیفتد به صورت ایده آل در این روش می توان از xk+1 پرش کرد به هر متغیری مانند xj که در سری وجود دارد رفت یا در بدترین حالت پیش آمده عمل پرش به xk+1 انجام پذیرد؛ که به این خانه، خانه پرش امن گفته می شود.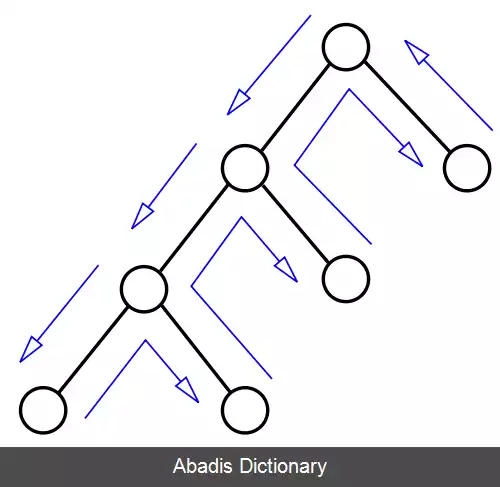

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر روش پس گرد زمانی که مقادیر یک متغیّر مورد بررسی قرار بگیرد و جستجو بی نتیجه پایان یابد، الگوریتم مقدار آخرین متغیرهای گره پیشین مورد بررسی قرار می دهد ولی اگر به انتها رسید و تمامی گره ها بررسی شد و به جواب درستی نرسیدیم، مقدار گره جستجو را تغییر و عملیات جستجو دوباره تکرار می شود. اگر شرایط به این گونه باشد x1=a1, …، xk =ak و تمامی مقادیر برای xk+1 بدون نتیجه برای پیدا کردن راه کار به پایان برسد الگوریتم یک سطح به بالا یعنی گره xk می رود؛ و در صورت امکان، مقدار را عوض کرده و به بالا بازمی گردد و سپس دوباره این مراحل را تکرار می کند.
انتخاب مقدار تخصیص جزئی xk+1 همواره به صورت کامل برای پیدا کردن راه حل ضروری نیست چرا که اجباراً ما را به سمت جواب پایانی هدایت نمی کند. اگر شرایط به این گونه باشد x1=a1, …xk=ak و تمامی مقادیر برای xk+1 بدون نتیجه برای پیدا کردن راه کار به پایان برسد الگوریتم یک سطح به بالا یعنی گره xk رفته و در صورت امکان مقدار را عوض کرده سپس دوباره این مراحل را تکرار می کند. انتخاب مقدار تخصیص جزئی xk+1 همواره به صورت کامل برای پیدا کردن راه حل ضروری نیست اما یک پیشوند تخصیص جزئی ممکن است در حل مسائل ارزش زیادی داشته باشد. برای این منظور از ایندکسهایی با شرط j < k استفاده می کنیم همانند x1, …، xj=a1, …، aj. این کار زمانی اتفاق می افتد که قابل بسط بیشتر برای ساختن یک راه حل برای xk+1 نیستیم. اگر الگوریتم بتواند اثبات کند این نکته را، می تواند به صورت مستقیم یک گره جدیدی برای xj به جای xk جدید انتخاب نماید.
میزان بهره وری الگوریتم پس پرش میزان پرش به عقبی است که می تواند اتفاق بیفتد به صورت ایده آل در این روش می توان از xk+1 پرش کرد به هر متغیری مانند xj که در سری وجود دارد رفت یا در بدترین حالت پیش آمده عمل پرش به xk+1 انجام پذیرد؛ که به این خانه، خانه پرش امن گفته می شود.






wiki: پس پرش (الگوریتم)
