پس انتشار[ ۱] ( انگلیسی: Backpropagation ) یا انتشار معکوس، روشی در یادگیری عمیق برای آموزش شبکه های عصبی پیشخور است ( روش های مشابهی برای آموزش سایر شبکه های عصبی مصنوعی به وجود آمده است ) . در این روش با استفاده از قاعده زنجیره ای، گرادیان تابع هزینه برای تک تک وزن ها محاسبه می شود. برای این کار برای محاسبه گرادیان هر لایه نسبت به تابع هزینه، از مشتق جزئی تابع هزینه نسبت به لایه بعدی استفاده می شود. در واقع از آخرین لایه ( نزدیک ترین لایه به خروجی ) محاسبه مشتق ها شروع می شود و تا ابتدای شبکه ( نزدیک ترین لایه به ورودی ها ) ادامه پیدا می کند.
روش معمول محاسبه گرادیان ( محاسبه اثر هر وزن در خروجی هر نمونه ) برای شبکه های عصبی پیشخور و به خصوص شبکه های عمیق بسیار زمان بر و در عمل غیرممکن است. با استفاده از روش پس انتشار و با کمک قاعده زنجیره ای و مشتق جزئی، در محاسبه گرادیان هر لایه از مشتقات لایه های جلوتر استفاده می شود و زمان اجرا تا حد زیادی کاهش پیدا می کند. [ ۲] استفاده از روش پس انتشار در کنار روش گرادیان کاهشی تصادفی، امکان اضافه کردن لایه های بیش تر به مدل به دلیل صرفه جویی زمانی به وجود می آید. این افزایش تعداد لایه ها از سوی دیگر باعث امکان یادگیری الگوهای پیچیده تر می شود.
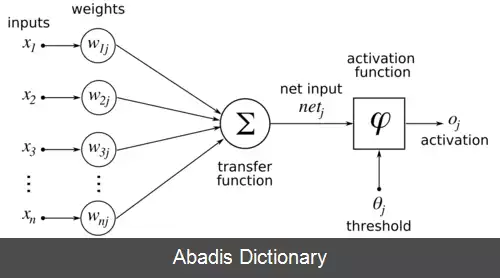
برای سلول عصبی c ورودیی که از سلول عصبی p به این سلول وارد می شود را با b p c نشان می دهیم. وزن این ورودی w p c است و مجموع ضرب ورودی ها با وزنهایشان را با a c نمایش می دهیم، یعنی a c = ∑ w p c × b p c . حال باید بر روی a c یک تابع غیر خطی اعمال کنیم، این تابع را θ c می نامیم و خروجی آن را با b c نمایش می دهیم به این معنی که b c = θ c ( a c ) . به همین شکل خروجی هایی که از سلول عصبی c خارج شده و به سلول n وارد می شوند را با b c n نمایش می دهیم و وزن آن را با w c n . اگر تمام وزنهای این شبکه عصبی را در مجموعه ای به اسم W بگنجانیم، هدف در واقع یادگیری این وزنهاست. [ ۳] اگر ورودی ما x باشد و خروجی y و خروجی شبکه عصبی ما h W ( x ) ، هدف ما پیدا کردن W است به قسمی که برای همه داده ها y و h W ( x ) به هم خیلی نزدیک شوند. به عبارت دیگر هدف کوچک کردن یک تابع ضرر بر روی تمام داده هاست، اگر داده ها را با ( x 1 , y 1 ) , ⋯ , ( x n , y n ) و تابع ضرر را با l نشان دهیم هدف کمینه کردن تابع پایین بر حسب W است:[ ۴]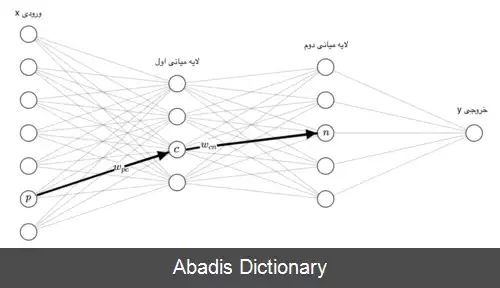
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفروش معمول محاسبه گرادیان ( محاسبه اثر هر وزن در خروجی هر نمونه ) برای شبکه های عصبی پیشخور و به خصوص شبکه های عمیق بسیار زمان بر و در عمل غیرممکن است. با استفاده از روش پس انتشار و با کمک قاعده زنجیره ای و مشتق جزئی، در محاسبه گرادیان هر لایه از مشتقات لایه های جلوتر استفاده می شود و زمان اجرا تا حد زیادی کاهش پیدا می کند. [ ۲] استفاده از روش پس انتشار در کنار روش گرادیان کاهشی تصادفی، امکان اضافه کردن لایه های بیش تر به مدل به دلیل صرفه جویی زمانی به وجود می آید. این افزایش تعداد لایه ها از سوی دیگر باعث امکان یادگیری الگوهای پیچیده تر می شود.
برای سلول عصبی c ورودیی که از سلول عصبی p به این سلول وارد می شود را با b p c نشان می دهیم. وزن این ورودی w p c است و مجموع ضرب ورودی ها با وزنهایشان را با a c نمایش می دهیم، یعنی a c = ∑ w p c × b p c . حال باید بر روی a c یک تابع غیر خطی اعمال کنیم، این تابع را θ c می نامیم و خروجی آن را با b c نمایش می دهیم به این معنی که b c = θ c ( a c ) . به همین شکل خروجی هایی که از سلول عصبی c خارج شده و به سلول n وارد می شوند را با b c n نمایش می دهیم و وزن آن را با w c n . اگر تمام وزنهای این شبکه عصبی را در مجموعه ای به اسم W بگنجانیم، هدف در واقع یادگیری این وزنهاست. [ ۳] اگر ورودی ما x باشد و خروجی y و خروجی شبکه عصبی ما h W ( x ) ، هدف ما پیدا کردن W است به قسمی که برای همه داده ها y و h W ( x ) به هم خیلی نزدیک شوند. به عبارت دیگر هدف کوچک کردن یک تابع ضرر بر روی تمام داده هاست، اگر داده ها را با ( x 1 , y 1 ) , ⋯ , ( x n , y n ) و تابع ضرر را با l نشان دهیم هدف کمینه کردن تابع پایین بر حسب W است:[ ۴]


wiki: پس انتشار
