تئوری پری داینامیک ( به انگلیسی: Peridynamics ) به عنوان زیر مجموعه علم مکانیک محیط های پیوسته ( به انگلیسی: Continuum Mechanics ) غیرموضعی، روشی است که در آن برای محاسبهٔ تنش به جای استفاده از مشتقات میدان جابجایی مستقیماً از میدان جابجایی استفاده می شود. برای این منظور هر جسم پیوسته در این تئوری به صورت گسسته مدل سازی می شود. بدین صورت که ذرات کروی شکلی که دارای حجم یکسانی می باشند، علاوه بر اینکه با در کنار هم قرار گرفتن شکل کلی جسم اولیه را ایجاد می کنند، بلکه دارای تبادلات نیرویی بوده و می توانند یکپارچگی مشابه با جسم پیوسته اولیه نیز ایجاد نمایند.
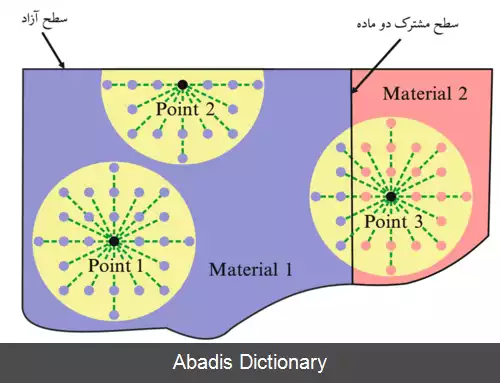
ایده اصلی و اولیهٔ این روش در مواجه با مشکل تعریف نشدگی مشتقات جزئی معادلات دیفرانسیل جزئی میدان جابجایی در سطوح ناپیوستگی، استفاده از انتگرال گیری به جای مشتق گیری در محاسبهٔ نیرو روی هر جزء از جسم است . از آنجایی که در معادلات موجود در این روش از مشتقات جزئی استفاده نمی شود، در سطوح ناپیوستگی این معادلات معتبر مانده و محدودیتی ایجاد نمی کنند. مدل ارائه شده در دستهٔ مدل های شامل اثرات غیرموضعی قرار می گیرد چرا که کل جسم به مجموعه ای ذرات در کنار هم تقسیم بندی شده و هر ذره با مجموعه ای از ذراتی که در همسایگی اش قرار دارند به صورت دو جفتی تبادل نیرویی دارد. با وجود این که تاکنون پژوهش های زیادی در زمینه اثرات غیر موضعی تنش صورت گرفته اما در اکثر آنها ایدهٔ حذف مشتقات جزئی مطرح نشده است. در معادلات پری داینامیک مختصات حالت آغازین ذرات را با X ( k ) ، حجم هر ذره را با V ( k ) و چگالی ذرات را نیز با ρ ( k ) نمایش می دهند. با توجه به یک دستگاه مختصات دکارتی ذره x ( k ) با تجربه کردن جابجایی u ( k ) به نقطه ای جدید در فضا منتقل می شود که با بردار مکان y ( k ) آن را نمایش می دهند. حرکت ذرات در این تئوری از توصیف لاگرانژی حرکت تبعیت کرده و جابجایی و بردار نیروهای بدنه ای را به صورت u ( x ( k ) , t ) و b ( x ( k ) , t ) نمایش داده می شوند . طبق این تئوری حرکت جسم با توجه به تعامل و نیروهای دوجفتی بین ذره x ( k ) و سایر ذرات سنجیده می شود؛ بنابراین تعداد بی شماری نیروی دو جفتی بین نقطهٔ x ( k ) و سایر نقاط وجود داشته که در نظر گرفتن همه آنها در محاسبات هزینه محاسباتی بسیار زیادی را تحمیل کرده که منطقی نمی باشد. بدین ترتیب با توجه به این که ذرات دورتر به صورت قابل توجهی اثر کمتری بر روی ذره مد نظر می گذارند، تبادلات نیرویی هر ذره در یک ناحیه موضعی که آن را هُرایزن ( افق ) می نامند در نظر می گیرند. در واقع در یک فضای سه بعدی، هُرایزن معادل کره ای به شعاع δ می باشد که ذرات درون این کره را خانوادهٔ ذره x ( k ) نامیده و با H ( x ( ( k ) ) آن را نمایش می دهند . تبادلات نیرویی بین ذرات وابسته به تغییر شکل جسم و خواص ساختاری ماده بوده که در این تئوری به صورت روابط متنوعی درنظر گرفته شده است. میزان اثرات غیرموضعی در این روش تابع اندازه شعاع ناحیه تبادل نیرویی یا همان هرایزن بوده که با کاهش مقدار آن می توان این روش را تبدیل به روشی موضعی کرد؛ بنابراین تئوری الاستیسیتهٔ کلاسیک را می توان حالتی خاص از تئوری پری داینامیک درنظر گرفت در جایی که مقدار δ به صفر میل می کند . اگر فضای اشغال شده توسط جسم در ساختار اولیه خود را ناحیه R بنامیم، T بردار حالت نیرو و b نمایانگر نیروی بدنه ای باشند. همچنین بردار مکان ساختار اولیه را با x و بردار مکان ساختار تغییر شکل یافته با x'، معادلهٔ حرکتی که توسط سیلینگ برای تئوری پری داینامیک ارائه شده به صورت زیر است:
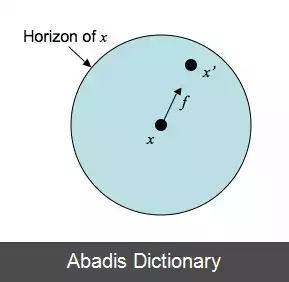
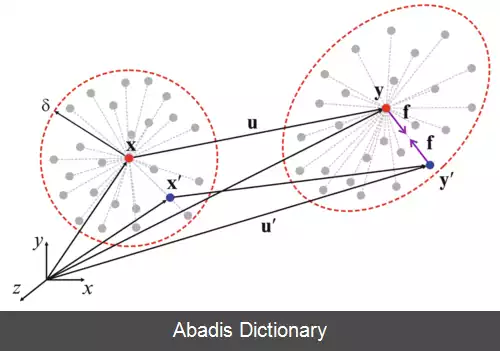
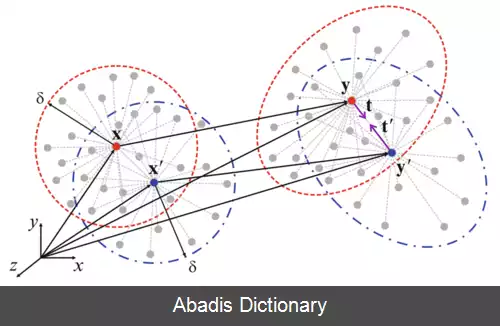
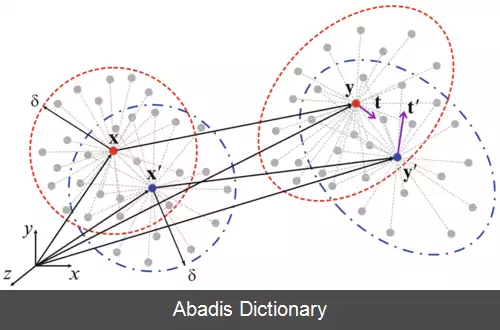
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفایده اصلی و اولیهٔ این روش در مواجه با مشکل تعریف نشدگی مشتقات جزئی معادلات دیفرانسیل جزئی میدان جابجایی در سطوح ناپیوستگی، استفاده از انتگرال گیری به جای مشتق گیری در محاسبهٔ نیرو روی هر جزء از جسم است . از آنجایی که در معادلات موجود در این روش از مشتقات جزئی استفاده نمی شود، در سطوح ناپیوستگی این معادلات معتبر مانده و محدودیتی ایجاد نمی کنند. مدل ارائه شده در دستهٔ مدل های شامل اثرات غیرموضعی قرار می گیرد چرا که کل جسم به مجموعه ای ذرات در کنار هم تقسیم بندی شده و هر ذره با مجموعه ای از ذراتی که در همسایگی اش قرار دارند به صورت دو جفتی تبادل نیرویی دارد. با وجود این که تاکنون پژوهش های زیادی در زمینه اثرات غیر موضعی تنش صورت گرفته اما در اکثر آنها ایدهٔ حذف مشتقات جزئی مطرح نشده است. در معادلات پری داینامیک مختصات حالت آغازین ذرات را با X ( k ) ، حجم هر ذره را با V ( k ) و چگالی ذرات را نیز با ρ ( k ) نمایش می دهند. با توجه به یک دستگاه مختصات دکارتی ذره x ( k ) با تجربه کردن جابجایی u ( k ) به نقطه ای جدید در فضا منتقل می شود که با بردار مکان y ( k ) آن را نمایش می دهند. حرکت ذرات در این تئوری از توصیف لاگرانژی حرکت تبعیت کرده و جابجایی و بردار نیروهای بدنه ای را به صورت u ( x ( k ) , t ) و b ( x ( k ) , t ) نمایش داده می شوند . طبق این تئوری حرکت جسم با توجه به تعامل و نیروهای دوجفتی بین ذره x ( k ) و سایر ذرات سنجیده می شود؛ بنابراین تعداد بی شماری نیروی دو جفتی بین نقطهٔ x ( k ) و سایر نقاط وجود داشته که در نظر گرفتن همه آنها در محاسبات هزینه محاسباتی بسیار زیادی را تحمیل کرده که منطقی نمی باشد. بدین ترتیب با توجه به این که ذرات دورتر به صورت قابل توجهی اثر کمتری بر روی ذره مد نظر می گذارند، تبادلات نیرویی هر ذره در یک ناحیه موضعی که آن را هُرایزن ( افق ) می نامند در نظر می گیرند. در واقع در یک فضای سه بعدی، هُرایزن معادل کره ای به شعاع δ می باشد که ذرات درون این کره را خانوادهٔ ذره x ( k ) نامیده و با H ( x ( ( k ) ) آن را نمایش می دهند . تبادلات نیرویی بین ذرات وابسته به تغییر شکل جسم و خواص ساختاری ماده بوده که در این تئوری به صورت روابط متنوعی درنظر گرفته شده است. میزان اثرات غیرموضعی در این روش تابع اندازه شعاع ناحیه تبادل نیرویی یا همان هرایزن بوده که با کاهش مقدار آن می توان این روش را تبدیل به روشی موضعی کرد؛ بنابراین تئوری الاستیسیتهٔ کلاسیک را می توان حالتی خاص از تئوری پری داینامیک درنظر گرفت در جایی که مقدار δ به صفر میل می کند . اگر فضای اشغال شده توسط جسم در ساختار اولیه خود را ناحیه R بنامیم، T بردار حالت نیرو و b نمایانگر نیروی بدنه ای باشند. همچنین بردار مکان ساختار اولیه را با x و بردار مکان ساختار تغییر شکل یافته با x'، معادلهٔ حرکتی که توسط سیلینگ برای تئوری پری داینامیک ارائه شده به صورت زیر است:






wiki: پری داینامیک
