در نظریه اتوماتا، شاخه ای از علوم کامپیوتر نظری، ماشین های تعیین پذیر حالات متناهی ( Deterministic finite - state machine ) به آن دسته از ماشین های حالات متناهی گفته می شود که رشته متناهی از سمبل ها را می پذیرد یا رد می کند و برای هر رشته ورودی تنها محاسباتی یکتا از ماشین اتوماتا را تولید می کند. در واقع 'تعیین پذیری' در این ماشین ها به یکتایی محاسبات برمی گردد. در جستجوی ساده ترین روش ها برای نمایش ماشین های حالت متناهی، مک کالک ( McCulloch ) و پیتس ( Pitts ) در میان اولین محققانی بودند که مفاهیم و ایده هایی شبیه به ماشین های اتوماتای محدود را در سال ۱۹۴۳ معرفی کردند.
شکل سمت چپ، یک ماشین تعین پذیر حالات متناهی را با استفاده از نمودار حالت ها نشان می دهد. در این ماشین اتوماتا، سه حالت S0، S1 و S2 وجود دارند ( که در تصویر با دایره نشان داده شده اند ) . ماشین اتوماتا دنباله ای از ۰ها و ۱ها را به عنوان ورودی دریافت می کند. برای هر حالت، به ازای هر یک از ۰ و ۱، یک بردار انتقال موجود است که به حالت بعد راهنمایی می کند. تا زمانی که یک نماد را می خوانیم، یک DFA به صورت تعیین پذیر و قطعی با دنبال کردن بردارهای انتقال از حالتی به حالت دیگر حرکت می کند. برای مثال، اگر ماشین اتوماتا در حالت S0 قرار دارد و نماد ورودی نیز ۱ است، به صورت قطعی به حالت S1 خواهد رفت. یک DFA دارای یک حالت آغازین است ( با فلشی که از هیچ کجا به آن وارد می شود، نشان داده می شود ) که محاسبات در آن آغاز می شوند، و یک مجموعه از حالات نهایی ( با دایره دوخطه نشان داده می شوند ) که کمک می کند زمانی را که محاسبات موفق شده است را تعریف کنیم. یک DFA به عنوان یک مفهوم ریاضی مطلق تعریف شده است، اما با توجه به ذات نعیین پذیر DFA، قابل پیاده سازی در سخت افزار و نرم افزار برای حل مسائلی خاص و مختلف است. برای مثال یک DFA می تواند یک نرم افزار را که تصمیم می گیرد که آیا ورودی کاربر ( برای مثال ) یک آدرس ایمیل معتبر است یا نه، مدل کند. DFAها دقیقاً مجموعه زبان های منظم را که، به غیر از موارد دیگر، برای انجام آنالیزهای واژگانی و تطبیق های الگویی مفید هستند، می پذیرند. همچنین DFAها می توانند از طریق ساخت مجموعه توانی از ماشین های تعین ناپذیر حالات متناهی ساخته شوند.
اتوماتون تعیین پذیر متناهی ( Deterministic Finite Automaton - DFA ) به یک پنج تائی M = ( Q , Σ , δ , q 0 , F ) گفته می شود، که شامل: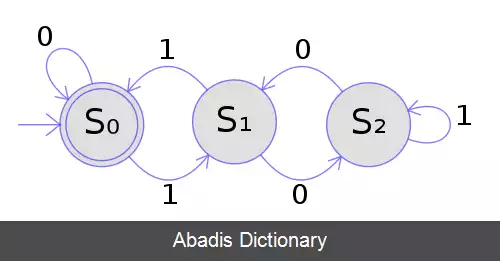
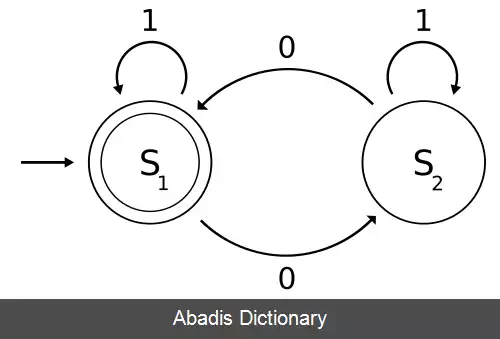
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفشکل سمت چپ، یک ماشین تعین پذیر حالات متناهی را با استفاده از نمودار حالت ها نشان می دهد. در این ماشین اتوماتا، سه حالت S0، S1 و S2 وجود دارند ( که در تصویر با دایره نشان داده شده اند ) . ماشین اتوماتا دنباله ای از ۰ها و ۱ها را به عنوان ورودی دریافت می کند. برای هر حالت، به ازای هر یک از ۰ و ۱، یک بردار انتقال موجود است که به حالت بعد راهنمایی می کند. تا زمانی که یک نماد را می خوانیم، یک DFA به صورت تعیین پذیر و قطعی با دنبال کردن بردارهای انتقال از حالتی به حالت دیگر حرکت می کند. برای مثال، اگر ماشین اتوماتا در حالت S0 قرار دارد و نماد ورودی نیز ۱ است، به صورت قطعی به حالت S1 خواهد رفت. یک DFA دارای یک حالت آغازین است ( با فلشی که از هیچ کجا به آن وارد می شود، نشان داده می شود ) که محاسبات در آن آغاز می شوند، و یک مجموعه از حالات نهایی ( با دایره دوخطه نشان داده می شوند ) که کمک می کند زمانی را که محاسبات موفق شده است را تعریف کنیم. یک DFA به عنوان یک مفهوم ریاضی مطلق تعریف شده است، اما با توجه به ذات نعیین پذیر DFA، قابل پیاده سازی در سخت افزار و نرم افزار برای حل مسائلی خاص و مختلف است. برای مثال یک DFA می تواند یک نرم افزار را که تصمیم می گیرد که آیا ورودی کاربر ( برای مثال ) یک آدرس ایمیل معتبر است یا نه، مدل کند. DFAها دقیقاً مجموعه زبان های منظم را که، به غیر از موارد دیگر، برای انجام آنالیزهای واژگانی و تطبیق های الگویی مفید هستند، می پذیرند. همچنین DFAها می توانند از طریق ساخت مجموعه توانی از ماشین های تعین ناپذیر حالات متناهی ساخته شوند.
اتوماتون تعیین پذیر متناهی ( Deterministic Finite Automaton - DFA ) به یک پنج تائی M = ( Q , Σ , δ , q 0 , F ) گفته می شود، که شامل:


wiki: پذیرنده متناهی معین
