پدیده گیبس ( به انگلیسی: Gibbs phenomenon ) یا پدیده گیبس - ویلبراهام به وجود نوسان در مقدار مجموع سری فوریه توابع در نزدیکی مقادیر ناپیوستگی گفته می شود. هر سیگنال متناوب را می توان به صورت جمعی از چند سیگنال نوسانی ساده ( سینوسی، کسینوسی یا نمایی ) با فرکانس های متفاوت نوشت. هرچقدر فرکانس یک سیگنال سازنده نسبت به سایر سیگنال ها بیشتر باشد آن سیگنال جزئیات بیشتری را نشان می دهد و از کلیات چشم می پوشد. برای همین هرچقدر تعداد هارمونیک های به کار رفته در شبیه سازی سیگنال اولیه بیشتر باشد، شکل ساخته شده جزئیات بیشتری را پوشش می دهد و در همه نقاط ( به خصوص نقاط مشتق ناپذیری که لبه ایجاد کرده اند ) سیگنال حاصل به سیگنال اصلی نزدیک تر خواهد بود، اگرچه هیچ گاه با مقدار اصلی تابع در آن محدوده دقیقاً برابر نخواهد شد و یک بازه عدم انطباق خواهیم داشت ( هرچند به آن بسیار نزدیک می شود ) . در واقع در سری فوریهٔ مربوط به شکل موج در نقاط ناپیوستگی مقدار سری فوریه برابر میانگین حد چپ و راست تابع در آن نقطه است ( در حالی که ممکن است مقدار تابع در آن نقطه چیزی متفاوت با آن باشد ) و به همین جهت در شکل سری فوریه تابع به سرعت به سمت این مقدار حرکت می کند که این امر موجب فراجهش یا بالازدگی می شود که به پدیدهٔ گیبس مشهور است. این پدیده اولین بار در سال ۱۸۴۸ توسط ویلبراهام مشاهده شده[ ۱] و پس از آن توسط گیبس در سال ۱۸۹۹[ ۲] [ ۳] [ ۴] معرفی شد و در سال ۱۹۰۶ توسط ماکسیم بوچر ( به انگلیسی: Maxime Bocher ) توضیح داده شد[ ۵] .
نمایش تقریبی سری فوریهٔ موج مربعی برای nهای دیگر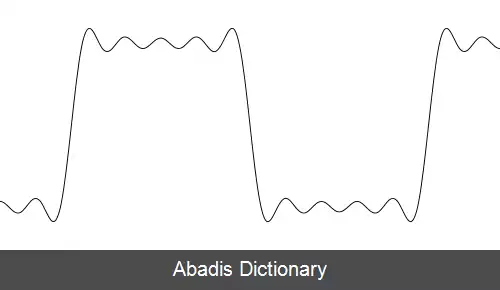
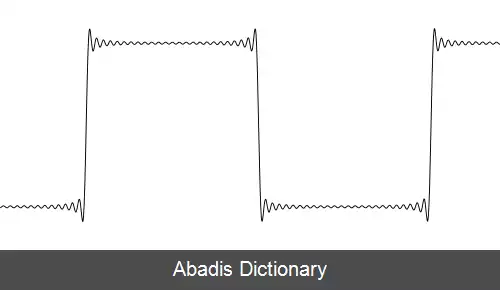
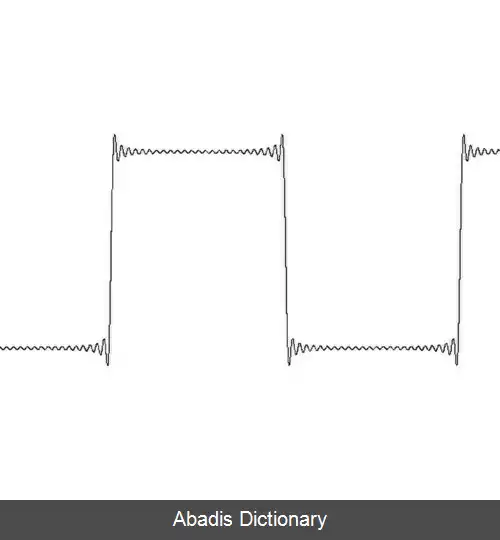
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنمایش تقریبی سری فوریهٔ موج مربعی برای nهای دیگر



wiki: پدیده گیبس
