پازل 8 تایی ( همچنین با "پازل جواهر"، "پازل رئیس جمهورها"، "بازی پانزده"، "مربع اسرارآمیز" و بسیاری اسامی دیگر نیز شناخته می شود ) یک پازل کشویی ( sliding puzzle ) است که از قابی با مربع های شماره گذاری شده که با ترتیبی تصادفی چیده شده اند در حالی که جای یکی از این مربع ها، خالی است. این پازل، در ابعاد مختلف وجود دارد، یکی از معروف ترین این پازل ها، پازل کوچکتر با نام پازل - ۸ می باشد. اگر ابعاد قاب 8x8 باشد، به پازل داده شده، پازل - ۸ یا پازل - 8 گفته می شود و اگر 8x8 باشد، به آن پازل - 8 یا پازل - 8 گفته می شود و به همین ترتیب برای ابعاد دیگر نیز نام گذاری انجام می شود. هدف این پازل این است که مربع ها را با استفاده از جا به جایی کشویی ( منظور انتقال هر مربع که کنار فضای خالی قرار دارد به فضای خالی می باشد ) ، مرتب کرد ( ترتیب مدنظر، از کوچکترین به بزرگترین است ) .
پازل - 8 یک مسئله کلاسیک در مدل کردن الگوریتم ها که شامل الگوریتم جستجوی کاشف می باشد. الگوریتم جستجوی کاشفی که معمولاٌ برای این مسئله استفاده می شود، شامل شمردن تعداد مربع هایی که در جای درست خود قرار ندارند و پیدا کردن حاصل جمع فاصله منهتن ( مجموع قدر مطلق تفاضل طول و عرض آن دو نقطه ) بین موقعیت هر مربع که در جای غلط قرار دارد با موقعیت همان مربع در چینش درست ( به ترتیب ) می شود.
در نظر داشته باشید که هر دو قابل قبول هستند، به عنوان مثال آن ها هیچوقت تعداد حرکات باقی مانده را مقداری بیشتر از واقعیت تخمین نمی زنند که باعث افزایش بازده الگوریتم های جستجو مثل A* می شود.
جانسون و استوری با استفاده از زوجیت نشان دادند که نصف چینش های ابتدایی برای پازل - n غیرقابل حل هستند؛ فرقی ندارد چه تعداد حرکت انجام شود. این کار از طریق تعریف کردن یک تابع از چینش کاشی ها که تحت هر حرکت قابل قبولی ناوردا است انجام میشود، و بعد با استفاده از این، فضای تمام حالت های نام گذاری شده را به دو کلاس هم ارز قابل دسترسی و غیر قابل دسترسی افراز می کنیم.
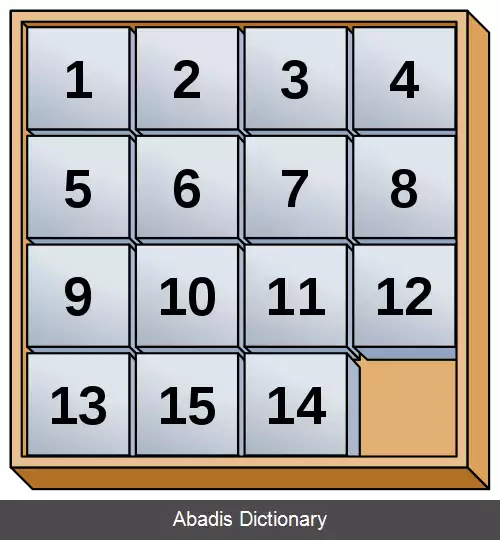
ناوردای موردنظر، زوجیت حاصل جمع جابجایی برای تمام شانزده مربع و زوجیت فاصله منهتن بین مربع خالی ( فضای خالی که توسط هیچ کاشی ای پر نشده است ) و گوشه ی پایین سمت راست است. دلیل ناوردا بودن این مقدار، این است که هر جابجایی زوجیت هردو مقدار جابجایی و فاصله منهتن را باهم تغییر می دهد. در حالت خاصی که مربع خالی در گوشه ی پایین سمت راست قرار داشته باشد، پازل حل پذیر است اگر و فقط اگر جابجایی قطعات باقی مانده زوج باشد.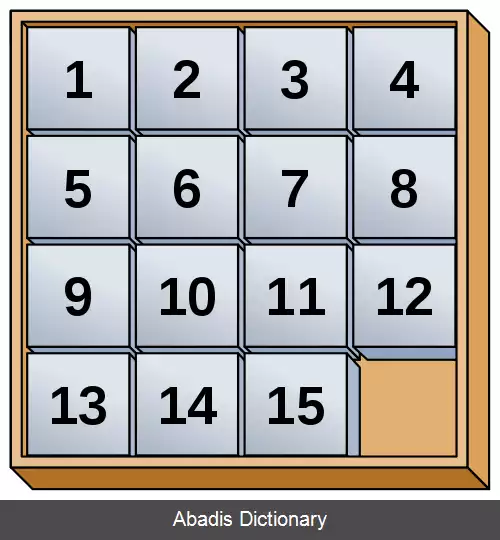

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفپازل - 8 یک مسئله کلاسیک در مدل کردن الگوریتم ها که شامل الگوریتم جستجوی کاشف می باشد. الگوریتم جستجوی کاشفی که معمولاٌ برای این مسئله استفاده می شود، شامل شمردن تعداد مربع هایی که در جای درست خود قرار ندارند و پیدا کردن حاصل جمع فاصله منهتن ( مجموع قدر مطلق تفاضل طول و عرض آن دو نقطه ) بین موقعیت هر مربع که در جای غلط قرار دارد با موقعیت همان مربع در چینش درست ( به ترتیب ) می شود.
در نظر داشته باشید که هر دو قابل قبول هستند، به عنوان مثال آن ها هیچوقت تعداد حرکات باقی مانده را مقداری بیشتر از واقعیت تخمین نمی زنند که باعث افزایش بازده الگوریتم های جستجو مثل A* می شود.
جانسون و استوری با استفاده از زوجیت نشان دادند که نصف چینش های ابتدایی برای پازل - n غیرقابل حل هستند؛ فرقی ندارد چه تعداد حرکت انجام شود. این کار از طریق تعریف کردن یک تابع از چینش کاشی ها که تحت هر حرکت قابل قبولی ناوردا است انجام میشود، و بعد با استفاده از این، فضای تمام حالت های نام گذاری شده را به دو کلاس هم ارز قابل دسترسی و غیر قابل دسترسی افراز می کنیم.
ناوردای موردنظر، زوجیت حاصل جمع جابجایی برای تمام شانزده مربع و زوجیت فاصله منهتن بین مربع خالی ( فضای خالی که توسط هیچ کاشی ای پر نشده است ) و گوشه ی پایین سمت راست است. دلیل ناوردا بودن این مقدار، این است که هر جابجایی زوجیت هردو مقدار جابجایی و فاصله منهتن را باهم تغییر می دهد. در حالت خاصی که مربع خالی در گوشه ی پایین سمت راست قرار داشته باشد، پازل حل پذیر است اگر و فقط اگر جابجایی قطعات باقی مانده زوج باشد.



wiki: پازل ۱۵
