پارادوکس دوستی اولین بار توسط اسکات فِلد ( به انگلیسی: Scott L. Feld ) در سال ۱۹۹۱ مطرح شد. این پارادوکس بیان می کند که بیشتر انسان ها تعداد دوستان کمتری از میانگین تعداد دوستان دوستانشان دارند. این پدیده می تواند نمونه ای از یک نمونه گیری نادرست باشد که در آن احتمال وجود کسانی که تعداد زیادی دوست دارند در بین دوست های یک فرد بالا است. پارادوکس دوستی ریشهٔ بسیاری از ویژگی های شبکه های اجتماعی است. به طور کلی این پارادوکس در جواب مسائل جامع شناسی مانند "چرا دوستانمان از ما ثروتمندتر هستند؟" و سوالاتی از این قبیل نیز مطرح می شود. همچنین این پارادوکس در باب دنبال کردن روند شیوع یک بیماری واگیردار هم کاربرد گسترده ای دارد. [ ۱]
اگرچه مسئلهٔ دوستی ظاهری متناقض نما دارد اما قابل اثبات توسط رابطه های ریاضی است و به طور مستقیم به نامساوی کوشی - شوارتز و نامساوی حسابی - هندسی مربوط است.
به طور دقیق در اثبات ریاضی این پدیده، شبکهٔ اجتماعی یک گراف سادهٔ بدون جهت G = ( V , E ) است که V مجموعهٔ رأس ها، و نشانگر افراد شبکه، و E مجموعهٔ یال های گراف و نشان دهندهٔ رابطهٔ دوستی بین دو فرد است. در این اثبات دوستی دوطرفه در نظرگرفته شده است. درجهٔ هر رأس d ( v ) برابر تعداد دوست های فرد متناظر آن رأس است.
ابتدا میانگین تعداد دوست های یک فرد محاسبه می شود به این صورت که تعداد کل روابط دوستی ( یال ها ) تقسیم بر تعداد افراد ( رأس ها می شود ) :
μ = ∑ v ∈ V d ( v ) | V | = 2 | E | | V |
سپس برای محاسبهٔ میانگین دوستان دوست یک فرد، فردی را به صورت تصادفی انتخاب کرده و از بین دوستان او نیز به صورت تصادفی یک فرد ( رأس ) را انتخاب کرده و درجهٔ رأس را محاسبه می کنیم. حاصل برابر خواهد بود با:
μ f = ∑ v ∈ V d ( v ) 2 2 | E | = μ + σ 2 μ
که σ برابر واریانس درجهٔ رأس ها است. برای گرافی که رأس هایش درجه های متفاوتی داشته باشند σ و μ مثبت اند و درنتیجه μ f > μ که همان صورت پارادوکس دوستی است.
یک روش تحلیل عبارتی که μ f را نتیجه می دهد این است که اگر ( u , v ) نشان دهندهٔ دوستی دو فرد u و v باشد آنگاه فرد u ادعا می کند دوستی دارد که d ( v ) تا دوست دارد. از آنجا که v دقیقاً d ( v ) عدد دوست دارد پس d ( v ) فرد ادعای مشابهی با u دارند، یعنی برای هر فرد v ، d ( v ) 2 عدد از این ادعای دوستی وجود دارد. حال اگر این مقدار را برای همهٔ رئوس جمع کنیم و تقسیم بر جمع همهٔ درجات ( تعداد کل دوستی های موجود ) کنیم μ f بدست می آید.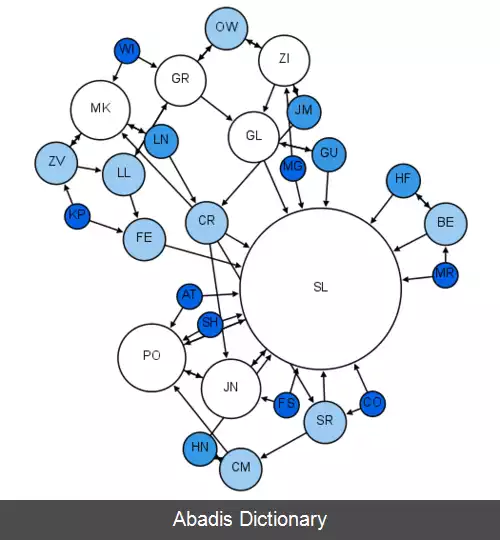
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگرچه مسئلهٔ دوستی ظاهری متناقض نما دارد اما قابل اثبات توسط رابطه های ریاضی است و به طور مستقیم به نامساوی کوشی - شوارتز و نامساوی حسابی - هندسی مربوط است.
به طور دقیق در اثبات ریاضی این پدیده، شبکهٔ اجتماعی یک گراف سادهٔ بدون جهت G = ( V , E ) است که V مجموعهٔ رأس ها، و نشانگر افراد شبکه، و E مجموعهٔ یال های گراف و نشان دهندهٔ رابطهٔ دوستی بین دو فرد است. در این اثبات دوستی دوطرفه در نظرگرفته شده است. درجهٔ هر رأس d ( v ) برابر تعداد دوست های فرد متناظر آن رأس است.
ابتدا میانگین تعداد دوست های یک فرد محاسبه می شود به این صورت که تعداد کل روابط دوستی ( یال ها ) تقسیم بر تعداد افراد ( رأس ها می شود ) :
μ = ∑ v ∈ V d ( v ) | V | = 2 | E | | V |
سپس برای محاسبهٔ میانگین دوستان دوست یک فرد، فردی را به صورت تصادفی انتخاب کرده و از بین دوستان او نیز به صورت تصادفی یک فرد ( رأس ) را انتخاب کرده و درجهٔ رأس را محاسبه می کنیم. حاصل برابر خواهد بود با:
μ f = ∑ v ∈ V d ( v ) 2 2 | E | = μ + σ 2 μ
که σ برابر واریانس درجهٔ رأس ها است. برای گرافی که رأس هایش درجه های متفاوتی داشته باشند σ و μ مثبت اند و درنتیجه μ f > μ که همان صورت پارادوکس دوستی است.
یک روش تحلیل عبارتی که μ f را نتیجه می دهد این است که اگر ( u , v ) نشان دهندهٔ دوستی دو فرد u و v باشد آنگاه فرد u ادعا می کند دوستی دارد که d ( v ) تا دوست دارد. از آنجا که v دقیقاً d ( v ) عدد دوست دارد پس d ( v ) فرد ادعای مشابهی با u دارند، یعنی برای هر فرد v ، d ( v ) 2 عدد از این ادعای دوستی وجود دارد. حال اگر این مقدار را برای همهٔ رئوس جمع کنیم و تقسیم بر جمع همهٔ درجات ( تعداد کل دوستی های موجود ) کنیم μ f بدست می آید.

wiki: پارادوکس دوستی
