واریته جبری ( به انگلیسی: algebraic variety ) ، اشیای مرکزی مورد مطالعه در هندسه جبری می باشند. به طور سنتی، یک واریته جبری به صورت مجموعه جواب های دستگاه معادلات چندجمله ای ها بر روی اعداد حقیقی یا مختلط تعریف می شوند. تعاریف مدرن این مفهوم را به چندین طریق گسترش می دهند، در حالی که سعی بر حفظ جنبه شهودی هندسی پشت تعریف اصلی را دارند.
قراردادهایی که در ارتباط با تعریف یک واریته جبری وجود دارد با هم کمی تفاوت دارند. به عنوان مثال، برخی از تعاریف نیازمند این هستند که یک واریته تحویل ناپذیر باشد؛ یعنی اجتماعی از دو مجموعهٔ کوچک تر بسته در توپولوژی زاریسکی نباشند. تحت این تعریف، واریته های جبری تحویل ناپذیر را مجموعه های جبری نیز گویند. قراردادهای دیگر، نیازی به مفهوم تحویل ناپذیری ندارند.
قضیه بنیادی جبر ارتباطی بین جبر و هندسه را برقرار می سازد، بدین طریق که: چندجمله ای تکین ( یک شیء جبری، چندجمله ای که ضریب بزرگ ترین توان آن یک باشد ) تک متغیره با ضرایب مختلط توسط مجموعه ریشه هایش ( شیئی هندسی ) تعیین می گردد. قضیه صفرهای هیلبرت با تعمیم این نتیجه، تناظری بنیادین بین ایده آل های حلقه های چندجمله ای و مجموعه های جبری برقرار می سازد. با استفاده از قضیه صفرهای هیلبرت و نتایج مرتبط، ریاضی دانان تناظری قوی بین سؤالات مربوط مجموعه های جبری و سؤالات مربوط به نظریه حلقه ها برقرار کرده اند.
بسیاری از واریته های جبری منیفلد هستند؛ ممکن است واریته های جبری نقاط تکین داشته باشند، در حالی که منیفلدها نمی توانند نقطه تکین داشته باشند. واریته های جبری را می توان با کمک ابعادشان شناسایی نمود. واریته های جبری از بعد یک را خم های جبری نامیده و واریته های جبری از بعد دو را رویه های جبری می نامند.
واریته آفین بر روی یک میدان بسته جبری، از نظر مفهومی راحت ترین نوع واریته ای است که می توان تعریف نمود. همچنین واریته های تصویری و شبه تصویری را می توان به شکل مشابهی تعریف نمود. کلی ترین تعریف یک واریته با به هم چسباندن تکه واریته های شبه تصویری به دست می آید. ساخت واریته های جدید به این شکل بدیهی و واضح نیست؛ اما ناگاتا مثالی از چنین واریته های جدیدی را در دهه ۱۹۵۰ میلادی ارائه نمود.
مقاله اصلی: واریته آفین
برای یک میدان جبری بسته مثل K و عددی طبیعی مثل n ، A n را یک n - فضای آفین بر روی K در نظر بگیرید. چندجمله ای های f در حلقه K را می توان به صورت توابع K - مقداری روی A n دید که مقادیرش را از نقاط A n بر می گیرد؛ یعنی هر x i نقطه ای از K انتخاب می کند. برای هر مجموعه S از چندجمله ای هایی در K ، مکان صفرهای آن یعنی Z ( S ) را مجموعه نقاطی از A n تعریف می کنیم که توابع داخل مجموعهٔ S هم زمان بر روی آن، صفر شوند، به عبارتی دیگر: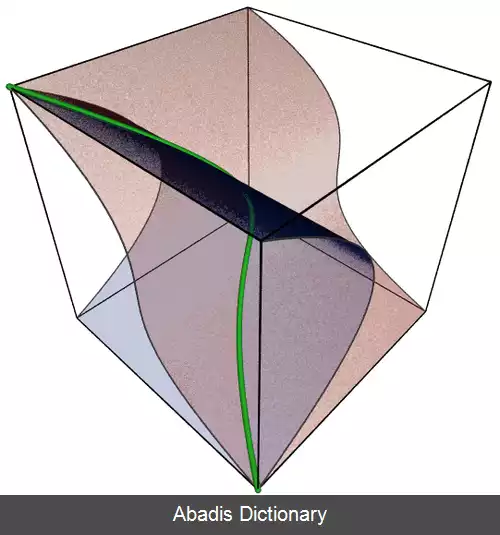
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفقراردادهایی که در ارتباط با تعریف یک واریته جبری وجود دارد با هم کمی تفاوت دارند. به عنوان مثال، برخی از تعاریف نیازمند این هستند که یک واریته تحویل ناپذیر باشد؛ یعنی اجتماعی از دو مجموعهٔ کوچک تر بسته در توپولوژی زاریسکی نباشند. تحت این تعریف، واریته های جبری تحویل ناپذیر را مجموعه های جبری نیز گویند. قراردادهای دیگر، نیازی به مفهوم تحویل ناپذیری ندارند.
قضیه بنیادی جبر ارتباطی بین جبر و هندسه را برقرار می سازد، بدین طریق که: چندجمله ای تکین ( یک شیء جبری، چندجمله ای که ضریب بزرگ ترین توان آن یک باشد ) تک متغیره با ضرایب مختلط توسط مجموعه ریشه هایش ( شیئی هندسی ) تعیین می گردد. قضیه صفرهای هیلبرت با تعمیم این نتیجه، تناظری بنیادین بین ایده آل های حلقه های چندجمله ای و مجموعه های جبری برقرار می سازد. با استفاده از قضیه صفرهای هیلبرت و نتایج مرتبط، ریاضی دانان تناظری قوی بین سؤالات مربوط مجموعه های جبری و سؤالات مربوط به نظریه حلقه ها برقرار کرده اند.
بسیاری از واریته های جبری منیفلد هستند؛ ممکن است واریته های جبری نقاط تکین داشته باشند، در حالی که منیفلدها نمی توانند نقطه تکین داشته باشند. واریته های جبری را می توان با کمک ابعادشان شناسایی نمود. واریته های جبری از بعد یک را خم های جبری نامیده و واریته های جبری از بعد دو را رویه های جبری می نامند.
واریته آفین بر روی یک میدان بسته جبری، از نظر مفهومی راحت ترین نوع واریته ای است که می توان تعریف نمود. همچنین واریته های تصویری و شبه تصویری را می توان به شکل مشابهی تعریف نمود. کلی ترین تعریف یک واریته با به هم چسباندن تکه واریته های شبه تصویری به دست می آید. ساخت واریته های جدید به این شکل بدیهی و واضح نیست؛ اما ناگاتا مثالی از چنین واریته های جدیدی را در دهه ۱۹۵۰ میلادی ارائه نمود.
مقاله اصلی: واریته آفین
برای یک میدان جبری بسته مثل K و عددی طبیعی مثل n ، A n را یک n - فضای آفین بر روی K در نظر بگیرید. چندجمله ای های f در حلقه K را می توان به صورت توابع K - مقداری روی A n دید که مقادیرش را از نقاط A n بر می گیرد؛ یعنی هر x i نقطه ای از K انتخاب می کند. برای هر مجموعه S از چندجمله ای هایی در K ، مکان صفرهای آن یعنی Z ( S ) را مجموعه نقاطی از A n تعریف می کنیم که توابع داخل مجموعهٔ S هم زمان بر روی آن، صفر شوند، به عبارتی دیگر:

wiki: واریته جبری
