واحدهای بازگشتی دروازه ای ( GRUs ) یک مکانیسم دروازه ای در شبکه های عصبی بازگشتی هستند که در سال ۲۰۱۴ توسط کیونگ هیون چو و همکارانش ایجاد شدند. [ ۱] واحد بازگشتی دروازه ای مانند یک حافظه طولانی کوتاه مدت ( LSTM ) با یک دروازه فراموشی کار می کند، [ ۲] اما پارامترهای کمتری نسبت به LSTM دارد، زیرا فاقد دروازه خروجی است. [ ۳] عملکرد GRU در برخی از وظایف مانند مدل سازی موسیقی چندصدایی، مدل سازی سیگنال گفتار و پردازش زبان طبیعی مشابه عملکرد LSTM است. [ ۴] [ ۵] GRUها عملکرد بهتری در مجموعه داده های کوچکتر و داده های کم بسامد دارند. [ ۶]
تغییرات مختلفی در واحد دروازه کامل وجود دارد، با استفاده از حالت مخفی قبلی و بایاس در ترکیب های مختلف، و یک شکل ساده به نام واحد حداقل دروازه ای.
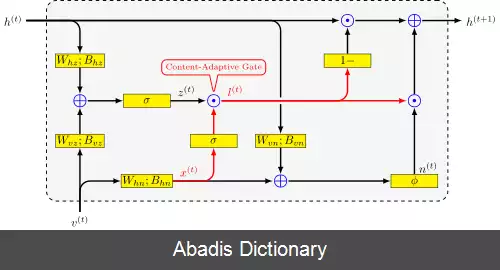
اپراتور ⊙ محصول هادامارد را در زیر نشان می دهد.
در ابتدا، برای t = 0 ، بردار خروجی عبارت است از h 0 = 0 .
• x t {\displaystyle x_{t}} : بردار ورودی
• h t {\displaystyle h_{t}} : بردار خروجی
• h ^ t {\displaystyle {\hat {h}}_{t}} : بردار فعال سازی
• z t {\displaystyle z_{t}} : بردار به روز رسانی
• r t {\displaystyle r_{t}} : بردار ریست
• W {\displaystyle W} ، U {\displaystyle U} و b {\displaystyle b} : ماتریس پارامتر و بردار
• σ g {\displaystyle \sigma _{g}} : تابع سیگموئید.
• ϕ h {\displaystyle \phi _{h}} : تابع هذلولی.
از سایر توابع فعال سازی نیز می توان استفاده کرد مشروط بر اینکه σ g ( x ) ∈ .
با تغییر z t و r t می توان شکلهای دیگری از مدل را ایجاد کرد:[ ۷]
• نوع اول، هر دروازه فقط به حالت پنهان قبلی و b بستگی دارد.
• نوع دوم، هر دروازه فقط به حالت پنهان قبلی بستگی دارد.
• نوع سوم، هر دروازه فقط با استفاده از b محاسبه می شود.
واحد حداقل دروازه ای مشابه واحد تمام دروازه ای است، به جز اینکه بردار به روز رسانی و ریست در یک دروازه فراموشی ادغام شده است. [ ۸]
• x t {\displaystyle x_{t}} : بردار ورودی
• h t {\displaystyle h_{t}} : بردار خروجی
• h ^ t {\displaystyle {\hat {h}}_{t}} : بردار فعال سازی
• f t {\displaystyle f_{t}} : بردار فراموشی
• W {\displaystyle W} ، U {\displaystyle U} و b {\displaystyle b} : ماتریس های پارامتر و بردار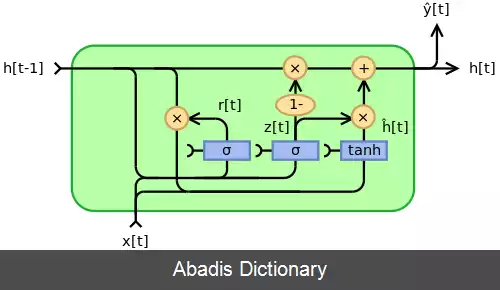
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتغییرات مختلفی در واحد دروازه کامل وجود دارد، با استفاده از حالت مخفی قبلی و بایاس در ترکیب های مختلف، و یک شکل ساده به نام واحد حداقل دروازه ای.
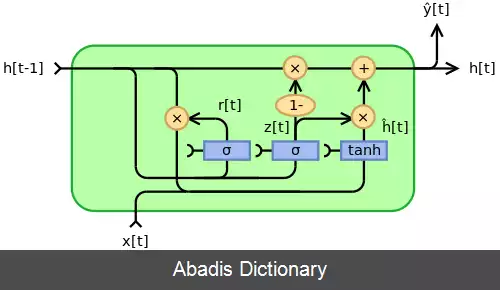
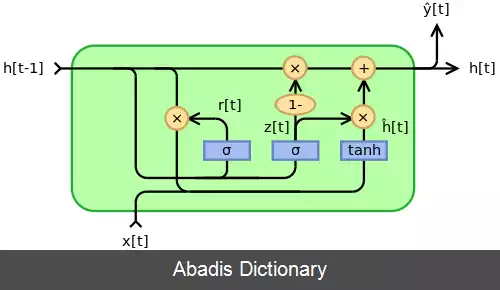
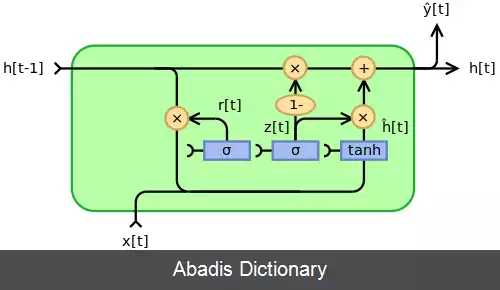
اپراتور ⊙ محصول هادامارد را در زیر نشان می دهد.
در ابتدا، برای t = 0 ، بردار خروجی عبارت است از h 0 = 0 .
• x t {\displaystyle x_{t}} : بردار ورودی
• h t {\displaystyle h_{t}} : بردار خروجی
• h ^ t {\displaystyle {\hat {h}}_{t}} : بردار فعال سازی
• z t {\displaystyle z_{t}} : بردار به روز رسانی
• r t {\displaystyle r_{t}} : بردار ریست
• W {\displaystyle W} ، U {\displaystyle U} و b {\displaystyle b} : ماتریس پارامتر و بردار
• σ g {\displaystyle \sigma _{g}} : تابع سیگموئید.
• ϕ h {\displaystyle \phi _{h}} : تابع هذلولی.
از سایر توابع فعال سازی نیز می توان استفاده کرد مشروط بر اینکه σ g ( x ) ∈ .
با تغییر z t و r t می توان شکلهای دیگری از مدل را ایجاد کرد:[ ۷]
• نوع اول، هر دروازه فقط به حالت پنهان قبلی و b بستگی دارد.
• نوع دوم، هر دروازه فقط به حالت پنهان قبلی بستگی دارد.
• نوع سوم، هر دروازه فقط با استفاده از b محاسبه می شود.
واحد حداقل دروازه ای مشابه واحد تمام دروازه ای است، به جز اینکه بردار به روز رسانی و ریست در یک دروازه فراموشی ادغام شده است. [ ۸]
• x t {\displaystyle x_{t}} : بردار ورودی
• h t {\displaystyle h_{t}} : بردار خروجی
• h ^ t {\displaystyle {\hat {h}}_{t}} : بردار فعال سازی
• f t {\displaystyle f_{t}} : بردار فراموشی
• W {\displaystyle W} ، U {\displaystyle U} و b {\displaystyle b} : ماتریس های پارامتر و بردار





wiki: واحد بازگشتی دروازه ای
