هندسه دیفرانسیل
فرهنگ فارسی
دانشنامه عمومی
هندسه دیفرانسیل شاخه ای از ریاضیات است که از تکنیک های حساب دیفرانسیل، حساب انتگرال، جبر خطی و جبر چندخطّی برای مطالعهٔ مسائل هندسی بهره می برد. نظریهٔ خم های مسطّح و فضایی و رویه های فضای اقلیدسی سه بعدی بنیانِ توسعهٔ هندسه دیفرانسیل را طی قرن هجدهم و نوزدهم میلادی تشکیل داد.
از اواخر قرن نوزدهم میلادی، هندسه دیفرانسیل رشد کرد و به شاخه ای تبدیل شد که دغدغهٔ آن ساختارهایِ عمومی تر روی منیفلدهای دیفرانسیل پذیر بود. هندسهٔ دیفرانسیل ارتباط نزدیکی با توپولوژی دیفرانسیل و جنبه های هندسی نظریهٔ معادلات دیفرانسیلی دارد. هندسهٔ دیفرانسیل رویه ها بسیاری از ایده ها و تکنیک هایِ کلیدی ذاتی این شاخه را در بر دارد.
• Ethan D. Bloch ( 27 June 2011 ) . A First Course in Geometric Topology and Differential Geometry. Springer Science & Business Media. ISBN 978 - 0 - 8176 - 8122 - 7.
• Burke, William L. ( 1985 ) . Applied Differential Geometry.
• do Carmo, Manfredo ( 1976 ) . Differential Geometry of Curves and Surfaces. ISBN 978 - 0 - 13 - 212589 - 5. Classical geometric approach to differential geometry without tensor analysis.
• do Carmo, Manfredo ( 1994 ) . Riemannian Geometry.
• Frankel, Theodore ( 2004 ) . The geometry of physics: an introduction ( 2nd ed. ) . ISBN 978 - 0 - 521 - 53927 - 2.
• Elsa Abbena; Simon Salamon; Alfred Gray ( 6 September 2017 ) . Modern Differential Geometry of Curves and Surfaces with Mathematica. CRC Press. ISBN 978 - 1 - 351 - 99220 - 6.
• Kreyszig, Erwin ( 1991 ) . Differential Geometry. ISBN 978 - 0 - 486 - 66721 - 8. Good classical geometric approach to differential geometry with tensor machinery.
• Kühnel, Wolfgang ( 2002 ) . Differential Geometry: Curves – Surfaces – Manifolds ( 2nd ed. ) . ISBN 978 - 0 - 8218 - 3988 - 1.
• McCleary, John ( 1994 ) . Geometry from a Differentiable Viewpoint.
• Spivak, Michael ( 1999 ) . A Comprehensive Introduction to Differential Geometry ( 5 Volumes ) ( 3rd ed. ) .
• ter Haar Romeny, Bart M. ( 2003 ) . Front - End Vision and Multi - Scale Image Analysis. ISBN 978 - 1 - 4020 - 1507 - 6.
• ریاضیات
• مقاله های خرد هندسه دیفرانسیل
• هندسه دیفرانسیل
• پردازش هندسی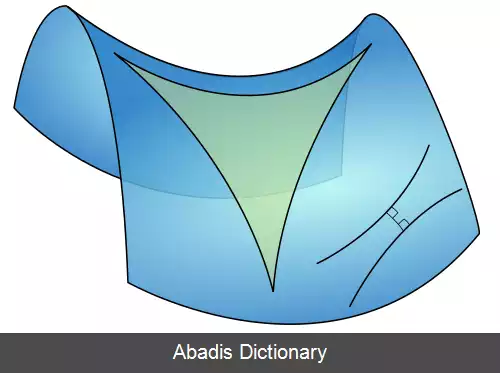
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاز اواخر قرن نوزدهم میلادی، هندسه دیفرانسیل رشد کرد و به شاخه ای تبدیل شد که دغدغهٔ آن ساختارهایِ عمومی تر روی منیفلدهای دیفرانسیل پذیر بود. هندسهٔ دیفرانسیل ارتباط نزدیکی با توپولوژی دیفرانسیل و جنبه های هندسی نظریهٔ معادلات دیفرانسیلی دارد. هندسهٔ دیفرانسیل رویه ها بسیاری از ایده ها و تکنیک هایِ کلیدی ذاتی این شاخه را در بر دارد.
• Ethan D. Bloch ( 27 June 2011 ) . A First Course in Geometric Topology and Differential Geometry. Springer Science & Business Media. ISBN 978 - 0 - 8176 - 8122 - 7.
• Burke, William L. ( 1985 ) . Applied Differential Geometry.
• do Carmo, Manfredo ( 1976 ) . Differential Geometry of Curves and Surfaces. ISBN 978 - 0 - 13 - 212589 - 5. Classical geometric approach to differential geometry without tensor analysis.
• do Carmo, Manfredo ( 1994 ) . Riemannian Geometry.
• Frankel, Theodore ( 2004 ) . The geometry of physics: an introduction ( 2nd ed. ) . ISBN 978 - 0 - 521 - 53927 - 2.
• Elsa Abbena; Simon Salamon; Alfred Gray ( 6 September 2017 ) . Modern Differential Geometry of Curves and Surfaces with Mathematica. CRC Press. ISBN 978 - 1 - 351 - 99220 - 6.
• Kreyszig, Erwin ( 1991 ) . Differential Geometry. ISBN 978 - 0 - 486 - 66721 - 8. Good classical geometric approach to differential geometry with tensor machinery.
• Kühnel, Wolfgang ( 2002 ) . Differential Geometry: Curves – Surfaces – Manifolds ( 2nd ed. ) . ISBN 978 - 0 - 8218 - 3988 - 1.
• McCleary, John ( 1994 ) . Geometry from a Differentiable Viewpoint.
• Spivak, Michael ( 1999 ) . A Comprehensive Introduction to Differential Geometry ( 5 Volumes ) ( 3rd ed. ) .
• ter Haar Romeny, Bart M. ( 2003 ) . Front - End Vision and Multi - Scale Image Analysis. ISBN 978 - 1 - 4020 - 1507 - 6.
• ریاضیات
• مقاله های خرد هندسه دیفرانسیل
• هندسه دیفرانسیل
• پردازش هندسی


wiki: هندسه دیفرانسیل
پیشنهاد کاربران
در بحث بالا یک کره حبابی هولوگرامی را مورد ملاحظه قرار دادیم و سطح آنرا با استفاده از روش دیفرانسیل جزئی هندسی به جزئیات بنیادی تقسیم کردیم. که مجموعه وسیعی از زوایای قائمه بودند و روی سطح کنار هم خوابیده بودند و ضلع سوم مثل تار و ریسمان از سقف آویزان گشته بودند. سطح کره را به دو لایه بسیار نازک و هر کدام به ضخامت یک خط یک بعدی هندسی تقسیم کردیم. طول اضلاع زاویه ها برابر بود با طول پلانک. این دو لایه طوریکه دیدیم هرکدام به دو بعدی های x, y بنیادی تجزیه شده بودند و استاد پلانک اجاز نمیداد آنها را بیشتر ریز کنیم. و x, y ها هم دو نوع بودند و روی سر دوتاشان هر کدام یک نقطه بود و نشان میداد که این از آن و آن از این مشتق پذیرند. بعد z هم که با همزادش z با نقطه آویزان بود و پا هایش به مرکز نمی رسید. t و t نقطه روی سر یکیشان هم سر جایشان قرار گرفته بودند. در گفتگوی یک طرفه پیشین، ریسمان و تارا هارا از سقف رها ساختیم که به سمت مرکز کره به مسابقه دوندگی به پردازند تا ببینیم کی زود تر به هدف خواهد رسید. در دنباله گفتگو کار دیگری انجام می دیم.
... [مشاهده متن کامل]
سام قرار است به ما کمک کند تا رسم حواله داده شده را مرسوم نمائیم. پیشنهاد سیمرغ این بود که به جای کره حبابی هولوگرامی، جام خیالی جهان نمای پیشدادیان را مورد ملاحظه قرار دهیم و سام هم پیشنهاد را پذیرفت و بر او احسن گفت و چون رای با اکثریت بود و من در اقلیت قرار داشتم، من هم موافقت کردم. هدف این مشورت این بود که این کره جام جهان نمای خیالی را به کوچکترین واحد هایش تقسیم کنیم و بین افراد خیالی آنها را تقسیم کنیم تا هر وقت که دلش خواست به آن نگاه کند و عکس کل و جزء را ببیند. تصمیم سام این بود که در این کار زار به رسم آبا و اجداد، یا با مشت و یا با پتک نریمان که از پدرش به ارس رسیده بود، جام را به گرد و غبار تبدیل کند و وزش باد ذرات آنرا به گوشه کناره های سرزمین ها با خود ببرد و هر خیالی ذره ای از آن دریافت کند. سیمرغ که مقوله هندسه و جزئیات و دیفرانسیل را شنیده بود، موافق رای سام نبود و میگفت در این میدان کار زار زور گردن و بازو نشاید، بلکه حساب دو دو تا چهار تاست، کار سهلی نیست. پس چه باید کرد ؟
پس از گفتگو های زیادی رای بر این شد که یک قطره نوشدارو روی آن بریزیم و منتظر معجزه به تماشای جام بنشینیم. به محض اینکه یک قطره نوشدارو از منقار سیمرغ روی آن کره حبابی هولوگرامی ریخته شد، شروع کرد تجزیه شدن.
سیمرغ میگفت این کار از طریق تقسیم بر دو صورت می گیرد و هر بار کل جزئیات سطح و بر دو تقسیم شده و ذرات آن هم که برای چشم شما ( من و سام ) ناپیداست در فضا پخش می شوند و فرشتگان آنها را به خیالات دیگران می رسانند. تا اینکه تقسیم به پایان رسید و بجای سطح چهار حلقه باقی ماند. بعد عرض و طول ( x, y ) روی همزاد های خود ( x, y با نقطه ) به دو حلقه عمود بر هم و بعد عمق z با همزادش هم به یک حلقه دیگر عمود بر آن دو حلقه تبدیل شده بود. این سه حلقه دارای دو محل تقاطع بودن و در آنجا با هم چهار زاویه ۹۰ در جه ای را تشکیل داده بودند. یک حلقه همسطح افق و یکی عمود بر سطح افق اما به سمت شمال و جنوب و حلقه سوم به سمت شرق و غرب. هر کدام از این دایره ها دو لایه داشتند که ضخامت آنها روی همدیگر برابر با ضخامت دو خط هندسی بود. البته سیمرغ آن تصاویر را بزرگنمایی میکرد و چشمان خیالی من و سام هم آنها را بطور آشکار میدند و ما از وقوع این معجزه لذت می بردیم . بعد زمان و بیزمانی هم روی به یک حلقه تبدیل شده بودند و با سه حلقه دیگر در محل تقاطع مماس بود. این چهار حلقه دو لایه ای جلوی چشم ما نوسان می کردند. سیمرغ میگفت که این حلقه ها میتوانند از هم جدا شوند و از هم دور گردند. جلوی چشم تماشا چیان که من و سام بودیم، سیمرغ یک قطره دیگر با منقار طلایی اش نوشدارو به سمت آن دایره ها پرتاب کرد و یک باره معجزه آسا همه از هم جدا شدند و دو باره لایه هم از هم جدا شدند و مجموعا به هشت حلقه جدا از تبدیل شدند. اما بعد از اینکه از هم جدا شدند، دست از رقصیدن و نوسان کردن بر داشتند و ساکن و بی حرکت سر جای خود در هوا جلوی چشم ما ایستادند. سیمرغ میگفت ببینید : محیط هرکدام از ۶ دایره های مکانی بیمکانی برابر است با طول پلانک و اگر محیط را بر حاصلضرب عدد ۲ در پی تقسیم کنیم آنگاه شعاع دایره بدست می آید و از طریق محاسبه حجم کره به مقدار حجمی می رسیم که برابر با ۲ � ۱۰ بتوان منهای ۱۰۷ متر خواهد بود. و در مورد دایره های زمانی و بیزمانی هم وضع چنین است حجمی که این دو حلقه در دوران دور مرکز ایجاد میکند برابر است با ۲� ۱۰ بتوان منهای ۱۳۱ . سیمرغ قبل از این محاسبات با دو قطره نوشدارو من و سام را در مقابل سرگیجه مصون نموده بود که با دیدن این ارقام غش نکنیم که در زیر سطح مطلق پلانک چه جواهراتی قائم شده اند. که علم انسان هنوز به این محاسبات شاید دست نزده باشد. سیمرغ میگفت که نظریه پردازان حلقه فقط چهار حلقه بی حیات و حرکت در دست دارند و تو سام هشت حلقه در دست. بنا براین سرمایه شناخت شما دو برابر سرمایه شناخت علمی آنهاست. آنها دارای یک خانواده چهار عضوی مقدس دارند و شما از این به بعد دو خانواده چهار عضوی مقدس و سماوی دارید. میگفت داشتن دو آدمک و دو حوا اک کافی نیست که با آن سرکی پشت پرده راز آسمانی، در عوض چهار آدمک و چهار حوا اک از هشت عضو تشکیل شده اند تولید مثل آنها هم معقول تر صورت می گیرد، تا یک آدمک و یک حوا اک و دو پسرک. و همچنین نظریه پردازان ریسمان کلاهشان پس معرکه گیر کرده است.
... [مشاهده متن کامل]
سام قرار است به ما کمک کند تا رسم حواله داده شده را مرسوم نمائیم. پیشنهاد سیمرغ این بود که به جای کره حبابی هولوگرامی، جام خیالی جهان نمای پیشدادیان را مورد ملاحظه قرار دهیم و سام هم پیشنهاد را پذیرفت و بر او احسن گفت و چون رای با اکثریت بود و من در اقلیت قرار داشتم، من هم موافقت کردم. هدف این مشورت این بود که این کره جام جهان نمای خیالی را به کوچکترین واحد هایش تقسیم کنیم و بین افراد خیالی آنها را تقسیم کنیم تا هر وقت که دلش خواست به آن نگاه کند و عکس کل و جزء را ببیند. تصمیم سام این بود که در این کار زار به رسم آبا و اجداد، یا با مشت و یا با پتک نریمان که از پدرش به ارس رسیده بود، جام را به گرد و غبار تبدیل کند و وزش باد ذرات آنرا به گوشه کناره های سرزمین ها با خود ببرد و هر خیالی ذره ای از آن دریافت کند. سیمرغ که مقوله هندسه و جزئیات و دیفرانسیل را شنیده بود، موافق رای سام نبود و میگفت در این میدان کار زار زور گردن و بازو نشاید، بلکه حساب دو دو تا چهار تاست، کار سهلی نیست. پس چه باید کرد ؟
پس از گفتگو های زیادی رای بر این شد که یک قطره نوشدارو روی آن بریزیم و منتظر معجزه به تماشای جام بنشینیم. به محض اینکه یک قطره نوشدارو از منقار سیمرغ روی آن کره حبابی هولوگرامی ریخته شد، شروع کرد تجزیه شدن.
سیمرغ میگفت این کار از طریق تقسیم بر دو صورت می گیرد و هر بار کل جزئیات سطح و بر دو تقسیم شده و ذرات آن هم که برای چشم شما ( من و سام ) ناپیداست در فضا پخش می شوند و فرشتگان آنها را به خیالات دیگران می رسانند. تا اینکه تقسیم به پایان رسید و بجای سطح چهار حلقه باقی ماند. بعد عرض و طول ( x, y ) روی همزاد های خود ( x, y با نقطه ) به دو حلقه عمود بر هم و بعد عمق z با همزادش هم به یک حلقه دیگر عمود بر آن دو حلقه تبدیل شده بود. این سه حلقه دارای دو محل تقاطع بودن و در آنجا با هم چهار زاویه ۹۰ در جه ای را تشکیل داده بودند. یک حلقه همسطح افق و یکی عمود بر سطح افق اما به سمت شمال و جنوب و حلقه سوم به سمت شرق و غرب. هر کدام از این دایره ها دو لایه داشتند که ضخامت آنها روی همدیگر برابر با ضخامت دو خط هندسی بود. البته سیمرغ آن تصاویر را بزرگنمایی میکرد و چشمان خیالی من و سام هم آنها را بطور آشکار میدند و ما از وقوع این معجزه لذت می بردیم . بعد زمان و بیزمانی هم روی به یک حلقه تبدیل شده بودند و با سه حلقه دیگر در محل تقاطع مماس بود. این چهار حلقه دو لایه ای جلوی چشم ما نوسان می کردند. سیمرغ میگفت که این حلقه ها میتوانند از هم جدا شوند و از هم دور گردند. جلوی چشم تماشا چیان که من و سام بودیم، سیمرغ یک قطره دیگر با منقار طلایی اش نوشدارو به سمت آن دایره ها پرتاب کرد و یک باره معجزه آسا همه از هم جدا شدند و دو باره لایه هم از هم جدا شدند و مجموعا به هشت حلقه جدا از تبدیل شدند. اما بعد از اینکه از هم جدا شدند، دست از رقصیدن و نوسان کردن بر داشتند و ساکن و بی حرکت سر جای خود در هوا جلوی چشم ما ایستادند. سیمرغ میگفت ببینید : محیط هرکدام از ۶ دایره های مکانی بیمکانی برابر است با طول پلانک و اگر محیط را بر حاصلضرب عدد ۲ در پی تقسیم کنیم آنگاه شعاع دایره بدست می آید و از طریق محاسبه حجم کره به مقدار حجمی می رسیم که برابر با ۲ � ۱۰ بتوان منهای ۱۰۷ متر خواهد بود. و در مورد دایره های زمانی و بیزمانی هم وضع چنین است حجمی که این دو حلقه در دوران دور مرکز ایجاد میکند برابر است با ۲� ۱۰ بتوان منهای ۱۳۱ . سیمرغ قبل از این محاسبات با دو قطره نوشدارو من و سام را در مقابل سرگیجه مصون نموده بود که با دیدن این ارقام غش نکنیم که در زیر سطح مطلق پلانک چه جواهراتی قائم شده اند. که علم انسان هنوز به این محاسبات شاید دست نزده باشد. سیمرغ میگفت که نظریه پردازان حلقه فقط چهار حلقه بی حیات و حرکت در دست دارند و تو سام هشت حلقه در دست. بنا براین سرمایه شناخت شما دو برابر سرمایه شناخت علمی آنهاست. آنها دارای یک خانواده چهار عضوی مقدس دارند و شما از این به بعد دو خانواده چهار عضوی مقدس و سماوی دارید. میگفت داشتن دو آدمک و دو حوا اک کافی نیست که با آن سرکی پشت پرده راز آسمانی، در عوض چهار آدمک و چهار حوا اک از هشت عضو تشکیل شده اند تولید مثل آنها هم معقول تر صورت می گیرد، تا یک آدمک و یک حوا اک و دو پسرک. و همچنین نظریه پردازان ریسمان کلاهشان پس معرکه گیر کرده است.
یک حباب شفاف هولوگرامی کروی شکل را در نظر بگیریم که فضای درون آن خالی از هر چیزی باشد. البته شکل های مکعب مربع و هشت ضلعی مربع شبیه حفره روی شان مومی کندوی زنبور عسل و یا حتا مخروط هم میتواند مورد تصور قرار گرفته شود. در اینجا وسیله و ابزار فقط قوه خیال و فکر و حواس محض، خط کش و پرگار و ابزار برش و جوشکاری همه در دست این قوا قرار دارند. با اندکی ملاحظه متوجه می شویم که سطح این شکل هندسی دارای دو بعد عرض و طول بوده و بعد عمق همه فضای کره را در بر گرفته است. البته این فرض که بعد عمق همه جای درونی این شکل هندسی را در تصرف خود دارد، در نگاه اول چنین به نظر میرسد. حال اندکی از فضای درونی خیال و فکر خودرا بیرون می کشیم و آنها را متوجه سطح کره متمرکز می نمائیم. سطح را از طریق دیفرانسیل هندسی ذهنی به بینهایت واحد های کوچک تفریق و تجزیه می نماییم ( عمل مشتق گیری جزئی را در فکر و خیال و حواس محض انجام میدهیم ) .
... [مشاهده متن کامل]
این واحد ها یا آجر های بنیادی که کل سطح از آنها ساخته شده است، هر کدام یک محور مختصات دو بعدی ( x, y ) اند که فقط دارای محور طول و عرض می بوده و محور عمق یا ( z ) در نقطه تقاطع هر سه محور به سمت درون و عمود بر نقطه تماس آویزان است و طول تا مرکز کره ادامه نمییابد. این بعد عمقی که تعداد آن در خیال و فکر و احساس غیر قابل شمارش اند، مثل تار یا ریسمان یک بعدی از سقف سطح به سمت مرکز کره آویزان اند و ریش درونی این بابای هندسی را به نمایش می گذراند. اگر از روی تفریح و تفنن خود را از طریق خیال در مرکز کره قرار دهیم و در هشت جهت ارض این گنبد مدور لاجوردی را از دیدگاه مبارک خویش مورد مشاهده مناظره قرار دهیم، در زیر سقف قوسی شکل فقط ریش می بینیم با مو های شسته رفته تک بعدی. این تار و ریسمان ها آنقدر بلند نیستند که سر آنها تا سطح ارض و پیش پای مشاهده گر برسند یا قد کشیده باشند. لذا در فکر و خیال هم دست دلمان به سر آن ریش های انبوه و مجلل آویزان شده از لایه درونی گنبد کبود نمیرسد چه رسد به لمس کردن با نوک ظریف انگشتان و بوییدن و مشام کشدیدن عطر و عبیر با ارگان بویایی و با بذاق چشیدن اطماع و با لبان بوسیدن آن نازنین تار ها و ریسمان ها که هیچ کدام دارای جعد و خم و پیچش حلقه وار ( تار یا ریسمان بسته ) نیستند.
حال چه کار کنیم ؟
کاری که اساتید برجسته از قبیل نیوتون و لایب نیتز از عهده آن بر نیامدند، استاد بر جسته دیگری به نام پلانک آنرا به پایان رساند. به مصداق معروف : کار آن کرد که آنرا به پایان رساند. طول هر کدام از تار های این چمن زار ریش برابر است با ۱۰ بتوان منهای ۳۵ متر و یا ۱۰ بتوان ۳۲ کیلومتر نا قابل. و طول و عرض دیگر همزادانشان که روی سطح سر نقطه ای پاهای های آنان را با سر نقطه ای پای خود نگه داشته و از سقوط و افتادن آنها جلوگیری میکنند که مبادا خدای نخواسته پس از رها شدن و تجربه حالت بی وزنی سر انجام طعمه مرکزیت شوند و توسط آن تقذیه و حل و محو گردند، همچنین برابرند با مقادیر بالا.
همه این تار ها چه تک و تنها آویزان به لایه درونی سقف و دو تایی عمود و خوابیده در روی سقف، فاقد حرکت و حیاط می باشند. جهت اینکه در پیشگاه جان حیاط بخش، در وسع خود زندگی و حرکت دریافت کنند ضروریست که دارای یک نظم مستعد دریافت حیاط شوند. برای ایجاد این نظم و مستعد نمودن ریشهای فاقد حرکت و حیاط، دو قلو های همزاد آنها را که از دوران پیشدادیان و باستان تاکنون در دیدگاه انسان خوابیده به نظر می رسیدند در افکار و احساسات و خیال در بخش محض بیدار نمائیم، خود این ریسمان و تار ها با ریسمان و تارهای هم زاد خویش از آغاز خلقت بیدار و همکار بوده اند و برای همیشه بیدار خواهند بود و الا حرکت و حیات در طبیعت و کیهان صورت نمیگرفت که همگی بطور عینی و واقعی شاهد آنیم . هرکدام از این تا رها دارای بعد زمانی خاص خویش میباشند که استاد محاسبات اندازه آنرا محاسبه کرده است و قدر آن برابر است با ۱۰ بتوان منهای ۴۳ ثانیه. با این وجود باز هم دارای استعداد خود حرکتی نمی باشند. اما استاد گرامی و ارجمند فاصله خالی بین ذرات مکان و زمان را مورد بررسی بیشتر و عمیق تر قرار نداده است و آنهم با این اشتباه در فکر و خیال که در طبیعت و کیهان فقط یک مختصات چهار بعدی وجود دارد. روزی از روز ها سیمرغ خیال از خود پرسید که این فواصل و فضای خالی بین ذرات از چه ماهیتی بر خوردار است ؟ آیا این فضای خالی پیوسته است و یا خود او هم از ذرات ساخته شده است. تا اینکه هاتف غیبی مثل همیشه گویا و خموش سر به بناگوش خیال او ندا داد که آنهم از ذرات تشکیل گردیده است. گفت یک لحظه تصور کن که دو ذره زمان پشت سر هم و دو ذره مکان در کنار همدیگر قرار گرفته باشند، آنگاه از خود به پرس که آیا این دو فاصله خالی و بی محتوا هستند یا دارای اصالت بیمکانی و بیزمانی اند. سیمرغ با شنیدن پچ پچ هاتف گویا از خواب غفلت در باب مکان و زمان بیدار شد و از هاتف پرسید، آیا این ذرات ناپیدا و غیبی اندازه و قدر و قَدَر هم دارند ؟ پاسخ شنید : اختیار داری ای مرغ مثل خودم ملکوتی، استاد که قبلا گفتیم که کار را تمام کرد و آنرا به انجام رسانید، کار را نیمه کاره رها کرده بود که تو آنرا به پایان کامل برسانی که دیگر نیاز به کارگر نداشته باشند، البته همه بیکار نمی شوند بلکه کار محاسباتی از نوع شروع خواهد شد و هزاران شغل و محل کار ایجاد خواهد شد و خمیازه کشیدن پشت میز کار و تحریر عده ای از همکاران به پایان میرسد و حیاتی نوین در وهم و خیال آنان دمیده خواهد شد.
البته که استاد یاد شده کار محاسباتی را ساده نموده است و میتوان روش اورا ادامه داد.
طول واحد های بنیادی ذرات بی مکانی و بی زمانی هر دو برابر اند با طول واحدهای بنیادی مکان و زمان استاد. این آجر ها و واحد های کوانتایی که روی هم قرار گیرند همان استعداد را دریافت خواهند کرد که موجب حرکت آنان میشود. هرکدام به یک نوسانگر زمانی و نوسانگر طولی تبدیل خواهند شد. دو بعد دیگر عمق و عرض هم در قالب حجم مکانی و بیمکانی به هم می پیوندند و به رقص و نوسان در میآیند.
دو قطب نوسانگر ها یک واحد متضاد در خویش را تشکیل میدهند که بطور دائمی و خسته نا پذیر جای همدیگر را از طریق حرکت دیالکتیکی به همدیگر هدیه می نمایند و از طریق القاء به همدیگر تبدیل میشوند که آنرا جبر یا ضرورت طبیعت نامند که ریشه و علت و عامل حرکت است. اما ریشه و عامل اصل خود حرکتی بحثی جداست و در این مقال اندک نمی گنجد.
حال بر گردیم به شکل هولوگرامی و کروی که در آغاز سخن ناچیز خود آنرا مورد مشاهده احساس و فکر و خیال محض قرار دادیم و داستان ریش های بی کار و بی حرکت. سطح دو بعدی اولیه و بدون زوج و حیات، هم اکنون دَمی شاد و تازه در پیکره سطحی خود بسان آه و یا دَم نو ( مثل پیامبر بزرگوار نوح و به پارسی نو آه یا دَم نو ) گرفته اند و به شور و هیجان و رقص و نو نسان در افتاده اند. سطح کره به یک موج محدود و بسته در خویش تبدیل شده است. که خود از دو سطح سه بعدی تنیده در هم تشکیل شده است که بطور دائم و خستگی ناپذیر جای همدیگر را به همدیگر هدیه می نمایند و به هم دیگر تبدیل میشوند و یا همدیگر در سر جای یکدیگر را القاء می کنند. فرکانس این نوسان برابر است با معکوس زمان استاد، یعنی ۱۰ بتوان ۴۳ بار در ثانیه. دو تا بعداز این دو مختصات سه بعدی، عرض و طول مکان و بیمکانی روی هم را ساخته اند و به بعد سوم دوقلوی همزاد زمان و بیزمانی هر کدام روی بعد مکانی و بیمکانی خود.
ریسمان ها و تار های قد کوتاه ( مثل ریش سه روزه ) که قبلا تک و تنها روی چهره سقف گنبد لاجوردی یا آبی خنک آویزان بودند، حال جملگی حال و هوایی دیگر بهشان دست می دهد هر تار که قبلا بی زوج و بی معشوق به سر می برد، همزاد خود را خود را آغوش میکشد و بوسه هایی جانانه نثار گونه های گل گون و لب های لعل فام محبوب و یا محبوبه خویش مینمایند و بیا و بین رقص رسما جلال را. این ذرات ریسمانی که اخیرا آنها را اشتباها ریسمان باز و یا بسته مثل حلقه می نامند دیگر نیازی به سقف و آویزان شدن از آنرا ندارند و همگی از چهره گنبد توسط دست رحمت و احیانا توسط تیغ تیز رحمت به سان ریش کنده شده رستم در غم و هجر فرزند دلیر و اخیرا با پشت به خاک خوابیده و حیات خویش را به جان حیات بخش سپرده و دل و جگر پدر را سوخته که در انتظار رسیدن نوشدارو در کنار فرزند از دست داده روزگار بی قرار نشسته، به همان سان کندن، تراشیده می شوند و تک تاز به سوی مرکز کره به راه می افتند و در این هجوم چه دست و پا ه و سر و کمرها که شکسته و یا خم نمیشوند.
از لحظه یا زمان صفر تا زمان استاد میلیاردها ها میلیارد سال انسانی گذشته است تا این رقاصان و نوسان گران ( گراویتون های تک بعدی ازلی ) با گرانش های کوانتومی حاصل از کنش و واکنش گران و گرانشی میل و رقبت به همدیگر و به محوب و محبوبه نقطه ای هندسی مرکزی، طول کشیده است که از این واحد ها که فقط از بعد طولی مکانی و بیمکانی و زمان و بیزمانی عمق تشکیل شده بودند، دو مختصات چهار بعدی را بسازند و گراویتون های ازلی چهار بعدی ( دو چهار بعدی در هم تنیده را ایجاد کنند. بقیه داستان را به سیمرغ خیال واگذار میکنم که سر وهم و خیال و عقل و فهم و فکر و احساس به صورت نزولی و صعودی به درد نیاور. در پایان این مرغ ملکوتی پیام میدهد که فرمول نهایی معروف همه چیز و همه کس فرمول بندی گردیده و بزودی خدمت شنودگان و گویندگان ایرانی و پارسی زبان عرض خواهد گردید. البته بدون تبعیض همه اقوام و ملیت های شریف دیگر هم میتوانند از آن بهره مند شوند و به سیمرغ خیال احسن و آفرین گویند، اگرم هدیه نفرمودند سیمرغ غمگین نمی گردد.
... [مشاهده متن کامل]
این واحد ها یا آجر های بنیادی که کل سطح از آنها ساخته شده است، هر کدام یک محور مختصات دو بعدی ( x, y ) اند که فقط دارای محور طول و عرض می بوده و محور عمق یا ( z ) در نقطه تقاطع هر سه محور به سمت درون و عمود بر نقطه تماس آویزان است و طول تا مرکز کره ادامه نمییابد. این بعد عمقی که تعداد آن در خیال و فکر و احساس غیر قابل شمارش اند، مثل تار یا ریسمان یک بعدی از سقف سطح به سمت مرکز کره آویزان اند و ریش درونی این بابای هندسی را به نمایش می گذراند. اگر از روی تفریح و تفنن خود را از طریق خیال در مرکز کره قرار دهیم و در هشت جهت ارض این گنبد مدور لاجوردی را از دیدگاه مبارک خویش مورد مشاهده مناظره قرار دهیم، در زیر سقف قوسی شکل فقط ریش می بینیم با مو های شسته رفته تک بعدی. این تار و ریسمان ها آنقدر بلند نیستند که سر آنها تا سطح ارض و پیش پای مشاهده گر برسند یا قد کشیده باشند. لذا در فکر و خیال هم دست دلمان به سر آن ریش های انبوه و مجلل آویزان شده از لایه درونی گنبد کبود نمیرسد چه رسد به لمس کردن با نوک ظریف انگشتان و بوییدن و مشام کشدیدن عطر و عبیر با ارگان بویایی و با بذاق چشیدن اطماع و با لبان بوسیدن آن نازنین تار ها و ریسمان ها که هیچ کدام دارای جعد و خم و پیچش حلقه وار ( تار یا ریسمان بسته ) نیستند.
حال چه کار کنیم ؟
کاری که اساتید برجسته از قبیل نیوتون و لایب نیتز از عهده آن بر نیامدند، استاد بر جسته دیگری به نام پلانک آنرا به پایان رساند. به مصداق معروف : کار آن کرد که آنرا به پایان رساند. طول هر کدام از تار های این چمن زار ریش برابر است با ۱۰ بتوان منهای ۳۵ متر و یا ۱۰ بتوان ۳۲ کیلومتر نا قابل. و طول و عرض دیگر همزادانشان که روی سطح سر نقطه ای پاهای های آنان را با سر نقطه ای پای خود نگه داشته و از سقوط و افتادن آنها جلوگیری میکنند که مبادا خدای نخواسته پس از رها شدن و تجربه حالت بی وزنی سر انجام طعمه مرکزیت شوند و توسط آن تقذیه و حل و محو گردند، همچنین برابرند با مقادیر بالا.
همه این تار ها چه تک و تنها آویزان به لایه درونی سقف و دو تایی عمود و خوابیده در روی سقف، فاقد حرکت و حیاط می باشند. جهت اینکه در پیشگاه جان حیاط بخش، در وسع خود زندگی و حرکت دریافت کنند ضروریست که دارای یک نظم مستعد دریافت حیاط شوند. برای ایجاد این نظم و مستعد نمودن ریشهای فاقد حرکت و حیاط، دو قلو های همزاد آنها را که از دوران پیشدادیان و باستان تاکنون در دیدگاه انسان خوابیده به نظر می رسیدند در افکار و احساسات و خیال در بخش محض بیدار نمائیم، خود این ریسمان و تار ها با ریسمان و تارهای هم زاد خویش از آغاز خلقت بیدار و همکار بوده اند و برای همیشه بیدار خواهند بود و الا حرکت و حیات در طبیعت و کیهان صورت نمیگرفت که همگی بطور عینی و واقعی شاهد آنیم . هرکدام از این تا رها دارای بعد زمانی خاص خویش میباشند که استاد محاسبات اندازه آنرا محاسبه کرده است و قدر آن برابر است با ۱۰ بتوان منهای ۴۳ ثانیه. با این وجود باز هم دارای استعداد خود حرکتی نمی باشند. اما استاد گرامی و ارجمند فاصله خالی بین ذرات مکان و زمان را مورد بررسی بیشتر و عمیق تر قرار نداده است و آنهم با این اشتباه در فکر و خیال که در طبیعت و کیهان فقط یک مختصات چهار بعدی وجود دارد. روزی از روز ها سیمرغ خیال از خود پرسید که این فواصل و فضای خالی بین ذرات از چه ماهیتی بر خوردار است ؟ آیا این فضای خالی پیوسته است و یا خود او هم از ذرات ساخته شده است. تا اینکه هاتف غیبی مثل همیشه گویا و خموش سر به بناگوش خیال او ندا داد که آنهم از ذرات تشکیل گردیده است. گفت یک لحظه تصور کن که دو ذره زمان پشت سر هم و دو ذره مکان در کنار همدیگر قرار گرفته باشند، آنگاه از خود به پرس که آیا این دو فاصله خالی و بی محتوا هستند یا دارای اصالت بیمکانی و بیزمانی اند. سیمرغ با شنیدن پچ پچ هاتف گویا از خواب غفلت در باب مکان و زمان بیدار شد و از هاتف پرسید، آیا این ذرات ناپیدا و غیبی اندازه و قدر و قَدَر هم دارند ؟ پاسخ شنید : اختیار داری ای مرغ مثل خودم ملکوتی، استاد که قبلا گفتیم که کار را تمام کرد و آنرا به انجام رسانید، کار را نیمه کاره رها کرده بود که تو آنرا به پایان کامل برسانی که دیگر نیاز به کارگر نداشته باشند، البته همه بیکار نمی شوند بلکه کار محاسباتی از نوع شروع خواهد شد و هزاران شغل و محل کار ایجاد خواهد شد و خمیازه کشیدن پشت میز کار و تحریر عده ای از همکاران به پایان میرسد و حیاتی نوین در وهم و خیال آنان دمیده خواهد شد.
البته که استاد یاد شده کار محاسباتی را ساده نموده است و میتوان روش اورا ادامه داد.
طول واحد های بنیادی ذرات بی مکانی و بی زمانی هر دو برابر اند با طول واحدهای بنیادی مکان و زمان استاد. این آجر ها و واحد های کوانتایی که روی هم قرار گیرند همان استعداد را دریافت خواهند کرد که موجب حرکت آنان میشود. هرکدام به یک نوسانگر زمانی و نوسانگر طولی تبدیل خواهند شد. دو بعد دیگر عمق و عرض هم در قالب حجم مکانی و بیمکانی به هم می پیوندند و به رقص و نوسان در میآیند.
دو قطب نوسانگر ها یک واحد متضاد در خویش را تشکیل میدهند که بطور دائمی و خسته نا پذیر جای همدیگر را از طریق حرکت دیالکتیکی به همدیگر هدیه می نمایند و از طریق القاء به همدیگر تبدیل میشوند که آنرا جبر یا ضرورت طبیعت نامند که ریشه و علت و عامل حرکت است. اما ریشه و عامل اصل خود حرکتی بحثی جداست و در این مقال اندک نمی گنجد.
حال بر گردیم به شکل هولوگرامی و کروی که در آغاز سخن ناچیز خود آنرا مورد مشاهده احساس و فکر و خیال محض قرار دادیم و داستان ریش های بی کار و بی حرکت. سطح دو بعدی اولیه و بدون زوج و حیات، هم اکنون دَمی شاد و تازه در پیکره سطحی خود بسان آه و یا دَم نو ( مثل پیامبر بزرگوار نوح و به پارسی نو آه یا دَم نو ) گرفته اند و به شور و هیجان و رقص و نو نسان در افتاده اند. سطح کره به یک موج محدود و بسته در خویش تبدیل شده است. که خود از دو سطح سه بعدی تنیده در هم تشکیل شده است که بطور دائم و خستگی ناپذیر جای همدیگر را به همدیگر هدیه می نمایند و به هم دیگر تبدیل میشوند و یا همدیگر در سر جای یکدیگر را القاء می کنند. فرکانس این نوسان برابر است با معکوس زمان استاد، یعنی ۱۰ بتوان ۴۳ بار در ثانیه. دو تا بعداز این دو مختصات سه بعدی، عرض و طول مکان و بیمکانی روی هم را ساخته اند و به بعد سوم دوقلوی همزاد زمان و بیزمانی هر کدام روی بعد مکانی و بیمکانی خود.
ریسمان ها و تار های قد کوتاه ( مثل ریش سه روزه ) که قبلا تک و تنها روی چهره سقف گنبد لاجوردی یا آبی خنک آویزان بودند، حال جملگی حال و هوایی دیگر بهشان دست می دهد هر تار که قبلا بی زوج و بی معشوق به سر می برد، همزاد خود را خود را آغوش میکشد و بوسه هایی جانانه نثار گونه های گل گون و لب های لعل فام محبوب و یا محبوبه خویش مینمایند و بیا و بین رقص رسما جلال را. این ذرات ریسمانی که اخیرا آنها را اشتباها ریسمان باز و یا بسته مثل حلقه می نامند دیگر نیازی به سقف و آویزان شدن از آنرا ندارند و همگی از چهره گنبد توسط دست رحمت و احیانا توسط تیغ تیز رحمت به سان ریش کنده شده رستم در غم و هجر فرزند دلیر و اخیرا با پشت به خاک خوابیده و حیات خویش را به جان حیات بخش سپرده و دل و جگر پدر را سوخته که در انتظار رسیدن نوشدارو در کنار فرزند از دست داده روزگار بی قرار نشسته، به همان سان کندن، تراشیده می شوند و تک تاز به سوی مرکز کره به راه می افتند و در این هجوم چه دست و پا ه و سر و کمرها که شکسته و یا خم نمیشوند.
از لحظه یا زمان صفر تا زمان استاد میلیاردها ها میلیارد سال انسانی گذشته است تا این رقاصان و نوسان گران ( گراویتون های تک بعدی ازلی ) با گرانش های کوانتومی حاصل از کنش و واکنش گران و گرانشی میل و رقبت به همدیگر و به محوب و محبوبه نقطه ای هندسی مرکزی، طول کشیده است که از این واحد ها که فقط از بعد طولی مکانی و بیمکانی و زمان و بیزمانی عمق تشکیل شده بودند، دو مختصات چهار بعدی را بسازند و گراویتون های ازلی چهار بعدی ( دو چهار بعدی در هم تنیده را ایجاد کنند. بقیه داستان را به سیمرغ خیال واگذار میکنم که سر وهم و خیال و عقل و فهم و فکر و احساس به صورت نزولی و صعودی به درد نیاور. در پایان این مرغ ملکوتی پیام میدهد که فرمول نهایی معروف همه چیز و همه کس فرمول بندی گردیده و بزودی خدمت شنودگان و گویندگان ایرانی و پارسی زبان عرض خواهد گردید. البته بدون تبعیض همه اقوام و ملیت های شریف دیگر هم میتوانند از آن بهره مند شوند و به سیمرغ خیال احسن و آفرین گویند، اگرم هدیه نفرمودند سیمرغ غمگین نمی گردد.
دیفرانسیل و اینتگرال هندسی اقتباسی است از دیفرانسیل و اینتگرال نیوتون و لایب نیتس ( یا لایبنیتز ) . در این رشته از ریاضی، اشکال هندسی تجزیه شده و به کوچکترین واحد ها یا آجر ها از هم گسیخته میشوند، مثلا یک مثلث هندسی تجزیه و تفریق میگردد تا کوچکترین مثلث ممکن حاصل شود که برابر است با سه نقطه بی بعد ریاضی به شکل یک مثلث در در کنار و هم. به همین ترتیب یک مخروط کله قندی هم میتواند به مخروط های بسیار ریزی تبدیل شود که قاعده و ارتفاع و سطح آن فقط از چند نقطه هندسی تشکیل شده باشد. هر کدام از این واحدهای نهائی پایین تر حد تفریق و تجزیه را می سازند و رسیدن به پائین تر از آن غیر ممکن می باشد. دیفرانسیل هندسی را می توان با یک بنا و یا معمار تخریب مقایسه کرد.
... [مشاهده متن کامل]
در عوض محاسبه اینتگرال هندسی این واحد های بسیار ریز را باهم جمع و ترکیب مینماید و شکل اولیه را ایجاد میکند. این محاسبه بین حد پایین که آجر باشد و حد بالا که ساختمان هندسی باشد عمل میکند. لذا اینتگرال هندسی را می توان با یک بنا و معمار سازنده و یا دوباره سازنده و یا خلق کننده نامید. مثل دو تا از خدایان هندو یکی کریشنا و دیگری شیوا، یکی میسازد و دیگری تخریب میکند و عمل از نو تکرار می شود.
محاسبات دیفرانسیل و اینتگرال حاصل خلاقیت آگاهی صاحبان آنان میباشد که امروز دیگران هم از آن استفاده میکنند. اما از آنجایی که آگاهی انسان ریشه در طبیعت دارد، لذا این محاسبات که بصورت مصنوعی توسط انسان شکل میگیرد، در اصل اقتباسی نا آگاهانه و یا آگاهانه از خود طبیعت است. بنا بر این خود طبیعت دارای یک رایانه همه جانبه است که در تمامی طول شبانه روز و در طی اعصار مختلف بطور خارقالعاده و خستگی ناپذیری این محاسبات را بدون لحظه ای استراحت و پشت گوش اندازی و بازی گوشی انجام میدهد. حد اکثر سرعت این رایانه برابر با سرعت نور می باشد و اثرات پیوندی و ناپیوندی یا اثرات جمع و ترکیب و یا تفریق و تجزیه برابر است با ثابت یا اثر کوانتوم پلانک. این رایانه را میتوان به بنا تشبیه کرد و ذرات اتمی را به مسالح و ابزار های کمی و کیفی. کمی از لحاظ جرم و کیفی از لحاظ میدان های الکترو مغناطیس و جذب و دفع الکتریکی مغناطیسی و جاذبه ها یا گرانش های جرمی. اما در ایجاد نظم ها و قالب های زنده و غیر زنده این این بنای طبیعی نقش معمار و طراح را نمیتواند بازی کند. این نظم ها تصادفی و احتمالی ایجاد نمی شوند بلکه از پیش توسط یک معمار طراحی و تعیین گردیده اند. میزان خطای نسبی و مطلق این محاسبات طبیعی در چار چوب اثر کوانتوم پلانک محدود میگردد. در چهارچوب زمان حال که برابر با ۱۰ بتوان منهای ۴۳ ثانیه میباشد ( زمان پلانک ) یک ذره کوانتومی ( ذرات نور مرئی و غیر مرئی و ذرات اتمی ) نمیتواند زودتر از ذره ای دیگر پا به صحنه و یا میدان آینده بگذارد و یا این حصار تنگ زمانی را شکسته و به گذشته باز گردد. همه اینها طبق باور ادیان قضا و قدر هاینند که آفریننده و خالق همه آنها را بطور مطلق و تغییر ناپذیر از پیش تعیین کرده است.
به این معنا که قبل از صدور امر خلقت و آفرینش گویا پیر دیر، خطاط و نقاش ازل ، کوژه گر دهر ، سرور همه شعبده باز ها ، سالار و سرور همه ساحرین و رمالان و سوژه نویس سوژه نوازان و بالاخره سردار و سالار سروران فرشتگان، بینهایت بار سکه ها و تاس ها را انداخته ودر پایان تاس بازی و سکه بازی به نتیجه مطلق رسیده و در بین راه باز گشت به خویشتن خویش نیازی به تاس بازی مجدد نیست. و لذا سکه را ما هر طوری به هوا بیندازیم همان روی خواهد آمد که از پیش تعیین شده است و فقط برای ما انسانها پنجاه در صد احتمال دارد.
عالمان علوم ریاضی ریاضی فیزیک می توانند یک سکه را در هوا بالا بیندازند و نتیجه را ببینند، اما در فضای بسیار ریز کوانتایی پلانک سکه مادی جای نمیگیرد و جای سکه بازی و تاس اندازی برای دلیران علم و شناخت خالی می باشد. در آن میدان بسیار تنگ سکه باز و تاس انداز کوانتومی اختیار و اراده آزاد از خود ندارد که آن بازی را به میل خود انجام دهد.
در پایان توجه خواننده را در همین صفحه به هندسه ریمانی عطف می نمایم. و اشاره ای کوتاه به ریشه حرکت در طبیعت می نمایم:
هندسه و فضا - زمان ریمانی ، مینکوفسکی، دِسیتر، و آنتی دِسیتر یا نوازش مانداسینا، فضا های کول آبی ( آبی خنک یا آبی لاجوردی، فضا - زمان ۱۱، ۱۶، ۲۶ بعدی نظریه های فرعی پنجگانه M زیر لوای نظریه ریسمان و دیفرانسیل فضای هندسی آشتِکار در نظریه حلقه همگی فاقد اصل خود حرکتی بوده و مخالفین آنها سعی میکنند توسط آگاهی خود بطور مصنوعی در موجودات از بیرون عنصر حرکت را به درون آن فضا - زمان ها قاچاق نمایند، بدون اینکه سعی کنند ریشه حرکت را در خود طبیعت جستجو کنند و نه در مخیله انسانی خود.
مختصات چهار بعدی فضا - زمان یا مکان - زمان
دارای یک مختصات فیزیکی همزاد می باشد که از باستان تا کنون از دید اندیشمندان پنهان مانده است. سه بعد بیمکانی این مختصات هر کدام دارای طولی برابر با طول پلانک و طول زمانی بعد بیزمانی آن برابر است با زمان پلانک.
بنابراین تا زمانیکه اندیشمندان این مختصات را در اینتگرال و دیفرانسیل هندسی خود در نظر نگیرند و آنرا هم ارزش با مختصات فضا - زمان معمولی ندانسته در محاسبات جای ندهند، فضا - زمان های آنان از زندگی یا از حرکت بر خوردار نخواهد شد.
... [مشاهده متن کامل]
در عوض محاسبه اینتگرال هندسی این واحد های بسیار ریز را باهم جمع و ترکیب مینماید و شکل اولیه را ایجاد میکند. این محاسبه بین حد پایین که آجر باشد و حد بالا که ساختمان هندسی باشد عمل میکند. لذا اینتگرال هندسی را می توان با یک بنا و معمار سازنده و یا دوباره سازنده و یا خلق کننده نامید. مثل دو تا از خدایان هندو یکی کریشنا و دیگری شیوا، یکی میسازد و دیگری تخریب میکند و عمل از نو تکرار می شود.
محاسبات دیفرانسیل و اینتگرال حاصل خلاقیت آگاهی صاحبان آنان میباشد که امروز دیگران هم از آن استفاده میکنند. اما از آنجایی که آگاهی انسان ریشه در طبیعت دارد، لذا این محاسبات که بصورت مصنوعی توسط انسان شکل میگیرد، در اصل اقتباسی نا آگاهانه و یا آگاهانه از خود طبیعت است. بنا بر این خود طبیعت دارای یک رایانه همه جانبه است که در تمامی طول شبانه روز و در طی اعصار مختلف بطور خارقالعاده و خستگی ناپذیری این محاسبات را بدون لحظه ای استراحت و پشت گوش اندازی و بازی گوشی انجام میدهد. حد اکثر سرعت این رایانه برابر با سرعت نور می باشد و اثرات پیوندی و ناپیوندی یا اثرات جمع و ترکیب و یا تفریق و تجزیه برابر است با ثابت یا اثر کوانتوم پلانک. این رایانه را میتوان به بنا تشبیه کرد و ذرات اتمی را به مسالح و ابزار های کمی و کیفی. کمی از لحاظ جرم و کیفی از لحاظ میدان های الکترو مغناطیس و جذب و دفع الکتریکی مغناطیسی و جاذبه ها یا گرانش های جرمی. اما در ایجاد نظم ها و قالب های زنده و غیر زنده این این بنای طبیعی نقش معمار و طراح را نمیتواند بازی کند. این نظم ها تصادفی و احتمالی ایجاد نمی شوند بلکه از پیش توسط یک معمار طراحی و تعیین گردیده اند. میزان خطای نسبی و مطلق این محاسبات طبیعی در چار چوب اثر کوانتوم پلانک محدود میگردد. در چهارچوب زمان حال که برابر با ۱۰ بتوان منهای ۴۳ ثانیه میباشد ( زمان پلانک ) یک ذره کوانتومی ( ذرات نور مرئی و غیر مرئی و ذرات اتمی ) نمیتواند زودتر از ذره ای دیگر پا به صحنه و یا میدان آینده بگذارد و یا این حصار تنگ زمانی را شکسته و به گذشته باز گردد. همه اینها طبق باور ادیان قضا و قدر هاینند که آفریننده و خالق همه آنها را بطور مطلق و تغییر ناپذیر از پیش تعیین کرده است.
به این معنا که قبل از صدور امر خلقت و آفرینش گویا پیر دیر، خطاط و نقاش ازل ، کوژه گر دهر ، سرور همه شعبده باز ها ، سالار و سرور همه ساحرین و رمالان و سوژه نویس سوژه نوازان و بالاخره سردار و سالار سروران فرشتگان، بینهایت بار سکه ها و تاس ها را انداخته ودر پایان تاس بازی و سکه بازی به نتیجه مطلق رسیده و در بین راه باز گشت به خویشتن خویش نیازی به تاس بازی مجدد نیست. و لذا سکه را ما هر طوری به هوا بیندازیم همان روی خواهد آمد که از پیش تعیین شده است و فقط برای ما انسانها پنجاه در صد احتمال دارد.
عالمان علوم ریاضی ریاضی فیزیک می توانند یک سکه را در هوا بالا بیندازند و نتیجه را ببینند، اما در فضای بسیار ریز کوانتایی پلانک سکه مادی جای نمیگیرد و جای سکه بازی و تاس اندازی برای دلیران علم و شناخت خالی می باشد. در آن میدان بسیار تنگ سکه باز و تاس انداز کوانتومی اختیار و اراده آزاد از خود ندارد که آن بازی را به میل خود انجام دهد.
در پایان توجه خواننده را در همین صفحه به هندسه ریمانی عطف می نمایم. و اشاره ای کوتاه به ریشه حرکت در طبیعت می نمایم:
هندسه و فضا - زمان ریمانی ، مینکوفسکی، دِسیتر، و آنتی دِسیتر یا نوازش مانداسینا، فضا های کول آبی ( آبی خنک یا آبی لاجوردی، فضا - زمان ۱۱، ۱۶، ۲۶ بعدی نظریه های فرعی پنجگانه M زیر لوای نظریه ریسمان و دیفرانسیل فضای هندسی آشتِکار در نظریه حلقه همگی فاقد اصل خود حرکتی بوده و مخالفین آنها سعی میکنند توسط آگاهی خود بطور مصنوعی در موجودات از بیرون عنصر حرکت را به درون آن فضا - زمان ها قاچاق نمایند، بدون اینکه سعی کنند ریشه حرکت را در خود طبیعت جستجو کنند و نه در مخیله انسانی خود.
مختصات چهار بعدی فضا - زمان یا مکان - زمان
دارای یک مختصات فیزیکی همزاد می باشد که از باستان تا کنون از دید اندیشمندان پنهان مانده است. سه بعد بیمکانی این مختصات هر کدام دارای طولی برابر با طول پلانک و طول زمانی بعد بیزمانی آن برابر است با زمان پلانک.
بنابراین تا زمانیکه اندیشمندان این مختصات را در اینتگرال و دیفرانسیل هندسی خود در نظر نگیرند و آنرا هم ارزش با مختصات فضا - زمان معمولی ندانسته در محاسبات جای ندهند، فضا - زمان های آنان از زندگی یا از حرکت بر خوردار نخواهد شد.
