در ریاضیات، برای دو گروه دلخواه ( G , ∗ ) و ( H , . ) ، هم ریختی گروهی ( به انگلیسی: Group Homomorphism ) از ( G , ∗ ) به ( H , . ) ، تابعی چون h : G → H است که برای تمام u , v ∈ G در خاصیت زیر صدق کند:
h ( u ∗ v ) = h ( u ) ⋅ h ( v )
که در آن عمل گروه سمت چپ معادله، مربوط به و عمل دوتایی سمت راست مربوط به است.
از این خاصیت می توان استنتاج کرد که عنصر همانی e G از را به عنصر همانی e H از می نگارد:
h ( e G ) = e H
همچنین این نگاشت، معکوس ها را به معکوس ها می برد، یعنی:
h ( u − 1 ) = h ( u ) − 1 .
ازین رو، می توان گفت که «با ساختار گروهی سازگار است».
در شاخه هایی از ریاضیات که گروه ها به ساختارهای دیگری نیز مجهز اند، برخی مواقع هم ریخی را به معنای نگاشتی در نظر می گیرند که نه تنها ساختار گروهی را حفظ کرده، بلکه ساختارهای دیگر آن مجموعه را نیز حفظ کند و با آن ها سازگاری داشته باشد؛ مثلاً همریختی بین گروه های توپولوژیکی را اغلب پیوسته در نظر می گیرند.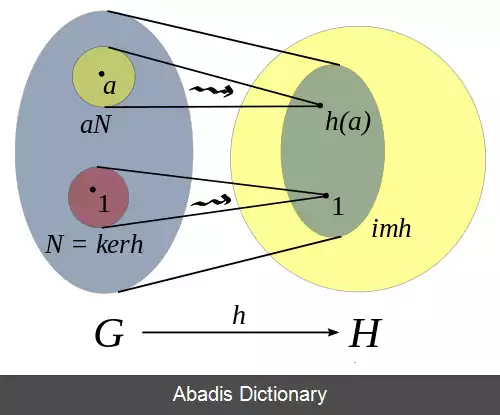
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفh ( u ∗ v ) = h ( u ) ⋅ h ( v )
که در آن عمل گروه سمت چپ معادله، مربوط به و عمل دوتایی سمت راست مربوط به است.
از این خاصیت می توان استنتاج کرد که عنصر همانی e G از را به عنصر همانی e H از می نگارد:
h ( e G ) = e H
همچنین این نگاشت، معکوس ها را به معکوس ها می برد، یعنی:
h ( u − 1 ) = h ( u ) − 1 .
ازین رو، می توان گفت که «با ساختار گروهی سازگار است».
در شاخه هایی از ریاضیات که گروه ها به ساختارهای دیگری نیز مجهز اند، برخی مواقع هم ریخی را به معنای نگاشتی در نظر می گیرند که نه تنها ساختار گروهی را حفظ کرده، بلکه ساختارهای دیگر آن مجموعه را نیز حفظ کند و با آن ها سازگاری داشته باشد؛ مثلاً همریختی بین گروه های توپولوژیکی را اغلب پیوسته در نظر می گیرند.

wiki: هم ریختی گروهی
