در نظریه بازی ها، هزینه پایداری ( به انگلیسی: price of stability یا PoS ) یک بازی به نسبت "بهترین هزینه اجتماعی تعادل های نش بازی" به "هزینهٔ اجتماعی حالت بهینه اجتماعی" گفته می شود. هدف از تعریف این نسبت پی بردن به این موضوع است که در یک بازی دخالت یک قدرت سوم برای خارج کردن رفتار بازیکنان از "خودخواه محض" بودن، به چه اندازه سودمند است. در کتاب دنیای جدید شجاع اثر آلدوس هاکسلی ( Aldous Huxley ) نیز اشاره ای به این مفهوم شده است. [ ۱] همچنین هنگامی که ما می خواهیم خوب و مؤثر بودن یک تعادل نش را در یک بازی خاص اندازه بگیریم، غالباً دربارهٔ هزینه آشوب ( PoA ) حرف می زنیم.
در یک بازی مفروض G با مجموعهٔ بازیکنان P و مجموعهٔ استراتژی های S، اگر {E:S^|P| - > {0, 1 یک تابع تعادل بوده و f یک تابع هدف باشد که معمولاً سودمحور ( به صورت جمع سودهای بازیکنان ) یا بیشینه محور ( به صورت بیشترین مقدار سود یک بازیکن ) تعریف می شود، آنگاه اگر S1 تا Sn مجموعهٔ همهٔ استراتژی پروفایل های تعادل باشند، منظور از هزینهٔ پایداری نسبت ( ( f ( S_i ) ) / ( f ( S ) است که در آن S_i تعادلی است که مقدار f را در میان سایر S_jها بیشینه می کند و S استراتژی پروفایلی است که مقدار f را بین همهٔ استراتژی پروفایل ها بیشینه می کند.
در کنار هزینهٔ پایداری، معیار دیگری نیز با عنوان هزینهٔ آشوب تعریف می شود که به معنی نسبت بدترین تعادل به حالت بهینهٔ تابع است.
به عبارتی هزینهٔ پایداری و هزینهٔ آشوب به همراه هم نشان می دهند اگر یک قدرت خارج از بازیکنان، آن ها را با قرار دادن سیاست هایی مجبور به انجام یکی دیگر از تعادلها کند، مقدار سود چقدر خواهد بود و اگر این کار را نکنند مقدار ضرر چقدر خواهد شد و در نهایت مشخص می شود که آیا این کار به صرفه هست یا نه. به طور خاص، هزینهٔ پایداری وقتی کاربردی است که بازیکنان برای دستیابی به یک حالت بهینه حاضر به همکاری هستند و مثالی خوب از هزینهٔ آشوب در اینترنت است که هر شرکت بدون در نظر گرفتن نفع جهانی در پی بیشینه کردن سود خود است.
همانگونه که گفته شد هزینه پایداری برابر است با بیشترین مقدار هزینهٔ اجتماعی تعادل های نش بازی تقسیم بر هزینهٔ اجتماعی در حالت بهینهٔ اجتماعی.
برای مثال در بازی معمای زندانی های زیر، تنها یک تعادل نش وجود دارد که عبارت است از ( عدم همکاری، عدم همکاری ) بنابراین داریم: هزینه پایداری = هزینه بی نظمی = ۱/۲.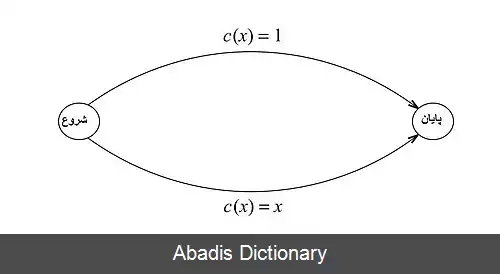
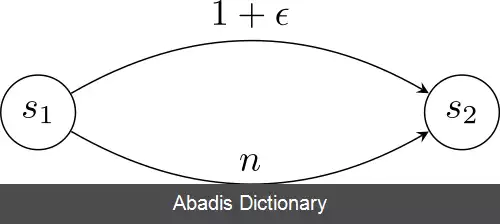
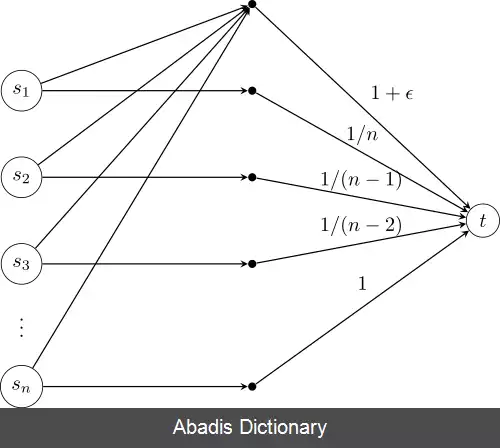
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر یک بازی مفروض G با مجموعهٔ بازیکنان P و مجموعهٔ استراتژی های S، اگر {E:S^|P| - > {0, 1 یک تابع تعادل بوده و f یک تابع هدف باشد که معمولاً سودمحور ( به صورت جمع سودهای بازیکنان ) یا بیشینه محور ( به صورت بیشترین مقدار سود یک بازیکن ) تعریف می شود، آنگاه اگر S1 تا Sn مجموعهٔ همهٔ استراتژی پروفایل های تعادل باشند، منظور از هزینهٔ پایداری نسبت ( ( f ( S_i ) ) / ( f ( S ) است که در آن S_i تعادلی است که مقدار f را در میان سایر S_jها بیشینه می کند و S استراتژی پروفایلی است که مقدار f را بین همهٔ استراتژی پروفایل ها بیشینه می کند.
در کنار هزینهٔ پایداری، معیار دیگری نیز با عنوان هزینهٔ آشوب تعریف می شود که به معنی نسبت بدترین تعادل به حالت بهینهٔ تابع است.
به عبارتی هزینهٔ پایداری و هزینهٔ آشوب به همراه هم نشان می دهند اگر یک قدرت خارج از بازیکنان، آن ها را با قرار دادن سیاست هایی مجبور به انجام یکی دیگر از تعادلها کند، مقدار سود چقدر خواهد بود و اگر این کار را نکنند مقدار ضرر چقدر خواهد شد و در نهایت مشخص می شود که آیا این کار به صرفه هست یا نه. به طور خاص، هزینهٔ پایداری وقتی کاربردی است که بازیکنان برای دستیابی به یک حالت بهینه حاضر به همکاری هستند و مثالی خوب از هزینهٔ آشوب در اینترنت است که هر شرکت بدون در نظر گرفتن نفع جهانی در پی بیشینه کردن سود خود است.
همانگونه که گفته شد هزینه پایداری برابر است با بیشترین مقدار هزینهٔ اجتماعی تعادل های نش بازی تقسیم بر هزینهٔ اجتماعی در حالت بهینهٔ اجتماعی.
برای مثال در بازی معمای زندانی های زیر، تنها یک تعادل نش وجود دارد که عبارت است از ( عدم همکاری، عدم همکاری ) بنابراین داریم: هزینه پایداری = هزینه بی نظمی = ۱/۲.



wiki: هزینه پایداری
