در هندسه، هرم مربع القاعده هرمی است که قاعده آن مربع باشد. اگر راس عمود بر بالای مرکز مربع قرار داشته باشد، یک هرم مربع راست است و دارای تقارن C4v است. اگر تمام ضلع هایش برابر باشد، هرم مربع متساوی الاضلاع است و اولین جسم جانسون یعنی J1 می باشد.
در هرم مربع القاعده ای با حجم V و ارتفاع h و ضلع قاعده l همواره حجم با با رابطه V = 1 3 l 2 h محاسبه می گردد.
در هرم مربع سمت راست، تمام اضلاع جانبی دارای طول یکسانی هستند، و اضلاع غیر از قاعده مثلث متساوی الساقین هستند.
در هرم مربع راست با طول ضلع قاعده l و ارتفاع h و مساحت کل A و حجم V همواره روابط زیر برقرارند:
و ضلع جانبی برابر با:
و ارتفاع مثلث های وجوه جانبی برابر با:
و زوایا بین وجوه برابر با:
• بین قاعده و وجهی جانبی: arctan ( 2 h l ) {\displaystyle \arctan \left ( {{2\, h} \over {l}}\right ) }
• بین دو وجه جانبی: arccos ( − l 2 l 2 + 4 h 2 ) {\displaystyle \arccos \left ( {{ - l^{2}} \over {l^{2}+4\, h^{2}}}\right ) }
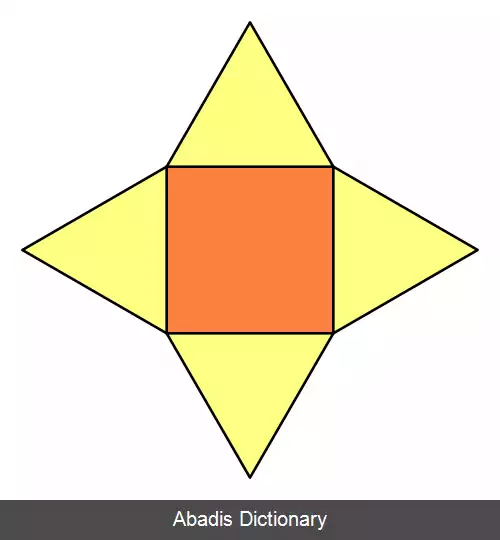
اگر تمام اضلاع دارای طول یکسانی باشند، وجوه جانبی هرم مثلث های متساوی الاضلاع هستند، و هرم، هرم مربع القاعده متساوی الاضلاع ( جسم جانسون J1 ) نامیده می شود.
اگر طول هر ضلع را l و ارتفاع را h و مساحت کل را A و حجم را V در نظر بگیریم همواره روابط زیر برقرارند:
• بین قاعده و وجهی جانبی: arctan ( 2 ) ≈ 54. 73561 ∘ . {\displaystyle \arctan {{\biggl ( }{\sqrt {2}}{\biggl ) }}\approx 54. 73561^{\circ }. }
• بین دو وجه جانبی: arccos ( − 1 3 ) ≈ 109. 47122 ∘ . {\displaystyle \arccos {\biggl ( }{ - 1 \over 3}{\biggl ) }\approx 109. 47122^{\circ }. }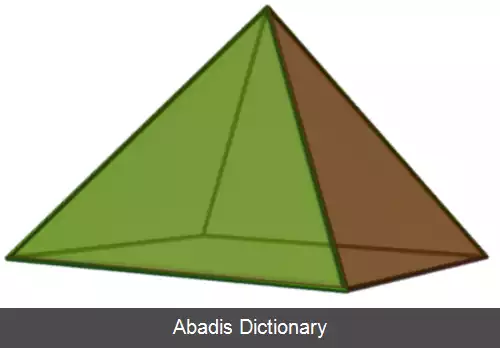
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر هرم مربع القاعده ای با حجم V و ارتفاع h و ضلع قاعده l همواره حجم با با رابطه V = 1 3 l 2 h محاسبه می گردد.
در هرم مربع سمت راست، تمام اضلاع جانبی دارای طول یکسانی هستند، و اضلاع غیر از قاعده مثلث متساوی الساقین هستند.
در هرم مربع راست با طول ضلع قاعده l و ارتفاع h و مساحت کل A و حجم V همواره روابط زیر برقرارند:
و ضلع جانبی برابر با:
و ارتفاع مثلث های وجوه جانبی برابر با:
و زوایا بین وجوه برابر با:
• بین قاعده و وجهی جانبی: arctan ( 2 h l ) {\displaystyle \arctan \left ( {{2\, h} \over {l}}\right ) }
• بین دو وجه جانبی: arccos ( − l 2 l 2 + 4 h 2 ) {\displaystyle \arccos \left ( {{ - l^{2}} \over {l^{2}+4\, h^{2}}}\right ) }
اگر تمام اضلاع دارای طول یکسانی باشند، وجوه جانبی هرم مثلث های متساوی الاضلاع هستند، و هرم، هرم مربع القاعده متساوی الاضلاع ( جسم جانسون J1 ) نامیده می شود.
اگر طول هر ضلع را l و ارتفاع را h و مساحت کل را A و حجم را V در نظر بگیریم همواره روابط زیر برقرارند:
• بین قاعده و وجهی جانبی: arctan ( 2 ) ≈ 54. 73561 ∘ . {\displaystyle \arctan {{\biggl ( }{\sqrt {2}}{\biggl ) }}\approx 54. 73561^{\circ }. }
• بین دو وجه جانبی: arccos ( − 1 3 ) ≈ 109. 47122 ∘ . {\displaystyle \arccos {\biggl ( }{ - 1 \over 3}{\biggl ) }\approx 109. 47122^{\circ }. }


wiki: هرم مربع القاعده
