در علوم کامپیوتر، هیپ فیبوناتچی به داده ساختار هیپی گفته می شود که شامل انبوهی از درخت ها است. این هیپ زمان اجرای سرشکن بهتری نسبت به هیپ دوجمله ای دارد. هیپ های فیبوناتچی توسط مایکل فردمن و رابرت تارجن در سال ۱۹۸۴ ایجاد شده اند، و برای اولین بار در یک مقاله علمی در سال ۱۹۸۷ منتشر شدند. ایده نام هیپ فیبوناتچی از اعداد فیبوناتچی که در اجرای تحلیل زمانی از آن استفاده می شود، گرفته شده است.
اعمال درج، یافتن کوچکترین مقدار، کاهش کلید، و ادغام ( الحاق ) در زمان سرشکن ثابت کار می کنند. اعمال حذف و حذف کوچکترین مقدار در زمان سرشکن O ( l o g n ) کار می کنند. این بدین معناست که با شروع از یک داده ساختار خالی، a عمل از دستورها گروه اول و b عمل از دستورها گروه دوم، زمان اجرای O ( a + b l o g n ) خواهد داشت. در هیپ های دو جمله انجام چنین عملی نیاز به زمان اجرای O ( ( a + b ) l o g ( n ) ) دارد؛ بنابراین زمانی که b از a کوچکتر باشد استفاده از هیپ فیبوناتچی به مراتب بهتر از استفاده از هیپ دوجمله ای است.
استفاده از هیپ های فیبوناتچی برای صف های اولویت دار زمان اجرای بعضی از الگوریتم های مهم را بهبود می بخشد، مثل الگوریتم دیکسترا برای محاسبه کوتاهترین مسیر در گراف، یا الگوریتم پریم برای محاسبه درخت فراگیر مینیمم در یک گراف.
هیپ فیبوناتچی مجموعه ای از درخت هاست خصوصیت مینیمم هیپ را داراست، به عبارتی، کلید فرزند همواره بزرگتر یا مساوی کلید پدر است؛ بنابراین کوچکترین کلید همواره در ریشهٔ یکی از درخت ها قرار دارد. در مقایسه با هیپ دو جمله ای، ساختار هیپ فیبوناتچی از قابلیت تغییرپذیری بیشتری برخوردار است. درخت ها شکل مشخصی ندارند و در بدترین حالت هیپ می تواند تمام عناصرش را در یک درخت جدا یا یک تک درخت با عمق n ذخیره کند. این قابلیت تغییرپذیری را می توان برای کند اجرا کردن برنامه ها به کار گرفت تا اجرای بعضی اعمال را به تأخیر انداخت. به طور مثال ادغام هیپ هارا می توان به آسانی با به هم پیوستن دو لیست از درخت ها انجام داد، و عمل کاهش کلید بعضی اوقات یک گره را از پدر جدا کرده و یک درخت جدید تشکیل می دهد.
با این حال در برخی موارد بعضی از دستورها نیاز دارند که برای رسیدن به زمان مورد نظر در حال اجرا به پشته معرفی شوند. به طور خاص، درجه گره ها ( در اینجا به معنی تعداد فرزندان ) را کم در نظر گرفته ایم: هر گره دارای درجه حداکثر O ( l o g n ) و اندازه زیر درخت گره از درجه k حداقل Fk + 2 است، که در آن Fk که k امین عدد فیبوناچی است. این امر از آنجا حاصل می شود که ما می توانیم حداکثر یک فرزند از هر گره غیرریشه را قطع کنیم. هنگامی که فرزند دوم قطع می شود، گره خود باید از پدر یا مادر خود بریده و تبدیل به ریشه درخت جدید شود ( در زیر می توانید اثبات مرزهای درجه را ببینید ) . تعداد درختان در عملیات حذف کوچکترین مقدار کاهش می یابد، که در آن درختان با هم مرتبط هستند.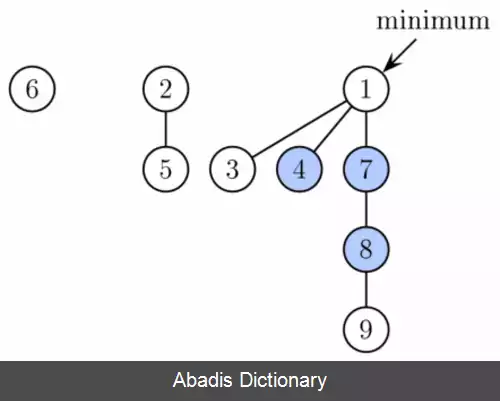
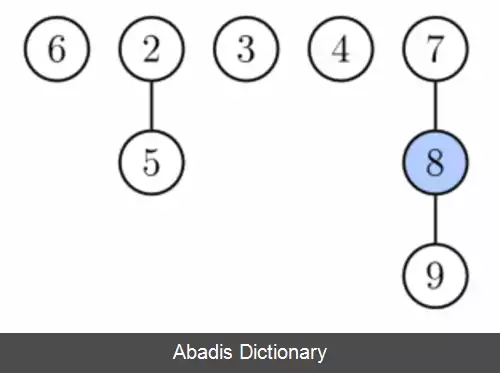
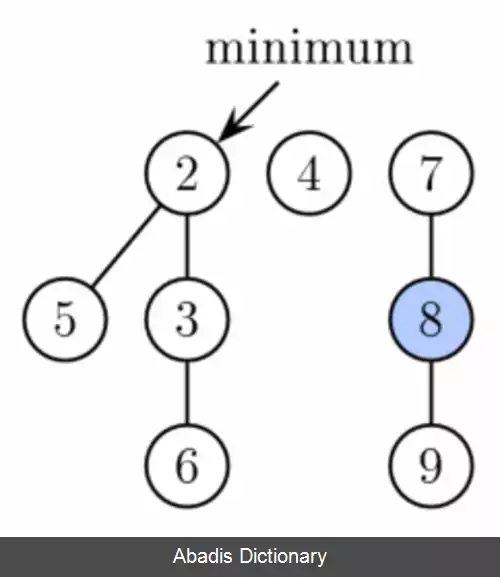
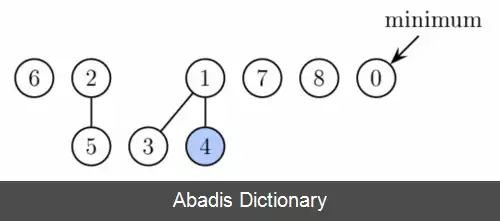
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاعمال درج، یافتن کوچکترین مقدار، کاهش کلید، و ادغام ( الحاق ) در زمان سرشکن ثابت کار می کنند. اعمال حذف و حذف کوچکترین مقدار در زمان سرشکن O ( l o g n ) کار می کنند. این بدین معناست که با شروع از یک داده ساختار خالی، a عمل از دستورها گروه اول و b عمل از دستورها گروه دوم، زمان اجرای O ( a + b l o g n ) خواهد داشت. در هیپ های دو جمله انجام چنین عملی نیاز به زمان اجرای O ( ( a + b ) l o g ( n ) ) دارد؛ بنابراین زمانی که b از a کوچکتر باشد استفاده از هیپ فیبوناتچی به مراتب بهتر از استفاده از هیپ دوجمله ای است.
استفاده از هیپ های فیبوناتچی برای صف های اولویت دار زمان اجرای بعضی از الگوریتم های مهم را بهبود می بخشد، مثل الگوریتم دیکسترا برای محاسبه کوتاهترین مسیر در گراف، یا الگوریتم پریم برای محاسبه درخت فراگیر مینیمم در یک گراف.
هیپ فیبوناتچی مجموعه ای از درخت هاست خصوصیت مینیمم هیپ را داراست، به عبارتی، کلید فرزند همواره بزرگتر یا مساوی کلید پدر است؛ بنابراین کوچکترین کلید همواره در ریشهٔ یکی از درخت ها قرار دارد. در مقایسه با هیپ دو جمله ای، ساختار هیپ فیبوناتچی از قابلیت تغییرپذیری بیشتری برخوردار است. درخت ها شکل مشخصی ندارند و در بدترین حالت هیپ می تواند تمام عناصرش را در یک درخت جدا یا یک تک درخت با عمق n ذخیره کند. این قابلیت تغییرپذیری را می توان برای کند اجرا کردن برنامه ها به کار گرفت تا اجرای بعضی اعمال را به تأخیر انداخت. به طور مثال ادغام هیپ هارا می توان به آسانی با به هم پیوستن دو لیست از درخت ها انجام داد، و عمل کاهش کلید بعضی اوقات یک گره را از پدر جدا کرده و یک درخت جدید تشکیل می دهد.
با این حال در برخی موارد بعضی از دستورها نیاز دارند که برای رسیدن به زمان مورد نظر در حال اجرا به پشته معرفی شوند. به طور خاص، درجه گره ها ( در اینجا به معنی تعداد فرزندان ) را کم در نظر گرفته ایم: هر گره دارای درجه حداکثر O ( l o g n ) و اندازه زیر درخت گره از درجه k حداقل Fk + 2 است، که در آن Fk که k امین عدد فیبوناچی است. این امر از آنجا حاصل می شود که ما می توانیم حداکثر یک فرزند از هر گره غیرریشه را قطع کنیم. هنگامی که فرزند دوم قطع می شود، گره خود باید از پدر یا مادر خود بریده و تبدیل به ریشه درخت جدید شود ( در زیر می توانید اثبات مرزهای درجه را ببینید ) . تعداد درختان در عملیات حذف کوچکترین مقدار کاهش می یابد، که در آن درختان با هم مرتبط هستند.




wiki: هرم فیبوناچی
