هرم دودویی یک داده ساختار هرم است که از یک درخت دودویی استفاده می کند. می توان به این داده ساختار به عنوان یک درخت دودویی نگاه کرد با این تفاوت که باید دو محدودیت را در نظر بگیریم. اول اینکه ای درخت، درخت دودویی کامل است، در همهٔ سطح های این درخت این ویژگی برقرار است به جز احتمالاً سطح اخر که در سطح اخر گره ها از چپ به راست پر هستند ( خاصیت ظاهری ) . و مورد دوم اینکه همه گره ها از فرزندشان کوچک ترمساوی ( یا بزرگ ترمساوی ) هستند. اگر همه گره ها از فرزندانشان کوچک ترمساوی باشند هرم کمینه و اگر همه گره ها بزرگ ترمساوی از فرزندانشان باشند هرم بیشینه نامگذاری می شوند ( خاصیت هرم ) . اغلب برای پیاده سازی صف اولویت از هرم کمینه استفاده می شود.
به این دلیل اینکه ترتیب فرزندان در هرم به طورمشخص نیست می توان جای آن ها را عوض کرد مگراینکه خاصیت ظاهری نقض شود.
هردو عمل درج و حذف در هرم دودویی در زمان ( O ( log n انجام می شود.
برای درج کردن الگوریتم به صورت زیر است:
• اضافه کردن عنصر جدید به سطح پایین هرم
• عنصر اضافه شده را با پدرش مقایسه کنید، اگر ترتیب آن ها درست بود الگوریتم متوقف می شود
• درغیراینصورت جای آن را با پدرش عوض می کنیم و سپس مرحله قبلی را تکرار می کنیم.
تعداد عملیات مورد نیاز به تعداد سطح هایی که عنصر جدید برای پیدا کردن مکان مناسب برای ارضا کردن ویژگی هرم باید طی کند بستگی دارد به همین دلیل به طور متوسط این عملیات در زمان ( O ( log n انجام می شود.
به عنوان مثال یک هرم بیشینه را در نظر بگیریم:
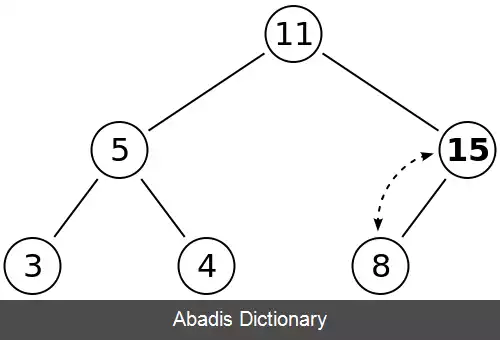
حال می خواهیم گره با کلید ۱۵ را درج کنیم:
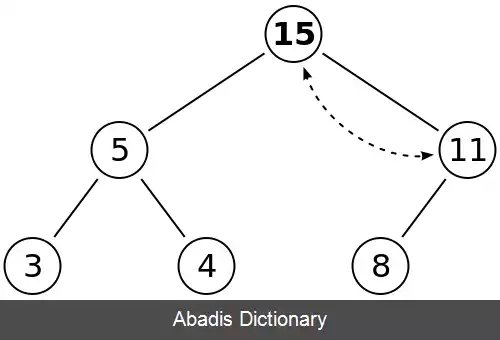
با توجه به اینکه هنوز ویژگی هرم بیشینه رعایت نشده است باید جای جای ریشه با فرزند سمت راست عوض کرد.
روش حذف کردن ریشه هرم و بازسازی هرم به منظور حفظ ویژگی آن پایین - هرم نامیده می شود که این روش به صورت زیر است:
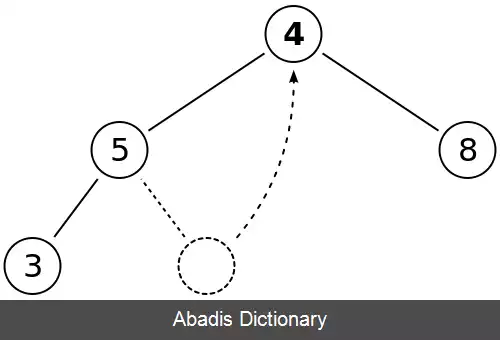
• ریشه هرم را با آخرین عنصر آخرین سطح جابه جا کنید
• مقایسه کنید ریشه را با فرزندانش اگر ویژگی هرم برقرار بود الگوریتم متوقف می شود
• در غیراینصورت جای ان را با فرزندانش عوض کنید و مرحله قبلی را تکرار کنید.
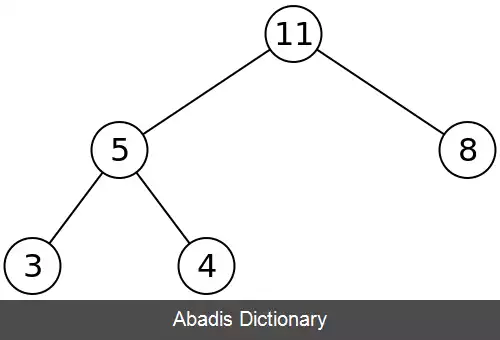
به عنوان مثال می خواهیم گره با کلید ۱۱ را حذف کنیم:
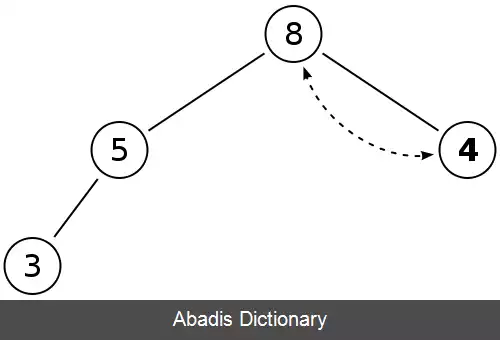
۱۱ را حذف می کنیم و با ۴ جابه جا می کنیم
حال مرحله ۳ الگوریتم را انجام می دهیم
در بدترین حالت ریشه جدید باید تا پایین ترین سطح بیاید تا ویژگی هرم برقرار شود، این جمله معنی می دهد که عملیات حذف با ارتفاع درخت رابطه دارد که به طور متوسط ( O ( log n است.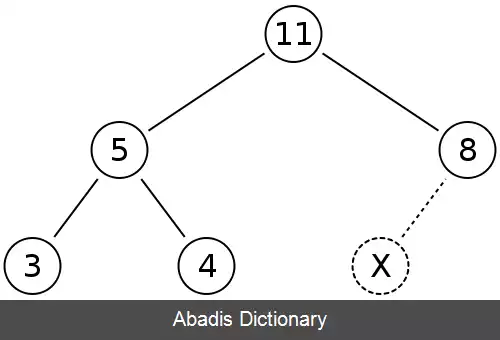
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه این دلیل اینکه ترتیب فرزندان در هرم به طورمشخص نیست می توان جای آن ها را عوض کرد مگراینکه خاصیت ظاهری نقض شود.
هردو عمل درج و حذف در هرم دودویی در زمان ( O ( log n انجام می شود.
برای درج کردن الگوریتم به صورت زیر است:
• اضافه کردن عنصر جدید به سطح پایین هرم
• عنصر اضافه شده را با پدرش مقایسه کنید، اگر ترتیب آن ها درست بود الگوریتم متوقف می شود
• درغیراینصورت جای آن را با پدرش عوض می کنیم و سپس مرحله قبلی را تکرار می کنیم.
تعداد عملیات مورد نیاز به تعداد سطح هایی که عنصر جدید برای پیدا کردن مکان مناسب برای ارضا کردن ویژگی هرم باید طی کند بستگی دارد به همین دلیل به طور متوسط این عملیات در زمان ( O ( log n انجام می شود.
به عنوان مثال یک هرم بیشینه را در نظر بگیریم:
حال می خواهیم گره با کلید ۱۵ را درج کنیم:
با توجه به اینکه هنوز ویژگی هرم بیشینه رعایت نشده است باید جای جای ریشه با فرزند سمت راست عوض کرد.
روش حذف کردن ریشه هرم و بازسازی هرم به منظور حفظ ویژگی آن پایین - هرم نامیده می شود که این روش به صورت زیر است:
• ریشه هرم را با آخرین عنصر آخرین سطح جابه جا کنید
• مقایسه کنید ریشه را با فرزندانش اگر ویژگی هرم برقرار بود الگوریتم متوقف می شود
• در غیراینصورت جای ان را با فرزندانش عوض کنید و مرحله قبلی را تکرار کنید.
به عنوان مثال می خواهیم گره با کلید ۱۱ را حذف کنیم:
۱۱ را حذف می کنیم و با ۴ جابه جا می کنیم
حال مرحله ۳ الگوریتم را انجام می دهیم
در بدترین حالت ریشه جدید باید تا پایین ترین سطح بیاید تا ویژگی هرم برقرار شود، این جمله معنی می دهد که عملیات حذف با ارتفاع درخت رابطه دارد که به طور متوسط ( O ( log n است.






wiki: هرم دودویی
