هرس آلفا بتا. هرس آلفا بتا الگوریتمی است که کارایی الگوریتم درخت Minimax ( درخت کمینه بیشینه یا درخت بازی ) را بهبود می بخشد. با استفاده از هرس آلفا بتا، بخش هایی از درخت کمینه بیشینه که پیمایششان بی تأثیر است پیمایش نمی شوند و به این ترتیب پیمایش درخت کمینه بیشینه تا یک عمق مشخص در زمانی کم تر صورت می گیرد.
برای بررسی ایدهٔ کلی هرس آلفا بتا این دو مسئلهٔ مشابه را در نظر بگیرید:
- تعدادی زیر مجموعهٔ ناتهی و متناهی از مجموعهٔ اعداد حقیقی در اختیار داریم. ارزش ( یا امتیاز ) هر یک از این مجموعه ها را برابر با کوچک ترین عضو آن تعریف می کنیم. هدفمان یافتن مجموعه ای با بیش ترین ارزش است.
فرض کنید که ارزش یکی از مجموعه ها برابر با m است. در این صورت مجموعه ای که دست کم یک عضو کوچک تر از m داشته باشد، پاسخ مسئله نخواهد بود. پس نیازی به بررسی اعضای این مجموعه ( و یافتن ارزش آن ) نیست. ( چرا که ارزش آن کوچک تر از m است )
- همان پرسش بالا را این گونه تغییر می دهیم: ارزش هر مجموعه برابر با بزرگ ترین عضو آن تعریف می شود و هدف یافتن کم ارزش ترین مجموعه است.
در این حالت نیز اگر مجموعه ای با ارزش m وجود داشته باشد مجموعه هایی که حداقل یک عضو بزرگ تر از m دارند، نمی توانند پاسخ مسئله باشند.
از همین ایده می توان برای بهینه کردن پیمایش روی درخت کمینه بیشینه بهره جست. شکل زیر را به عنوان بخشی از یک درخت کمینه بیشینه در نظر بگیرید:
فرض کنید ارزش ( امتیاز ) راس سبز را برابر با بیش ترین ارزش نسبت داده شده به فرزندان آن راس تعریف کنیم و ( مطابق با تعریف درخت کمینه بیشینه ) ارزش راس قرمز برابر با کم ترین ارزش نسبت داده شده به فرزندان آن راس تعریف شود. حال اگر هدف یافتن ارزش راس سبز باشد، نیازی به پیمایش زیر درخت راس قرمز و یافتن ارزش این راس نیست. چرا که ارزش راس قرمز حداکثر برابر ۳ می باشد در حالی که راس سبز فرزندی با ارزش ۵ دارد.
یکی از راه های پیاده سازی درخت کمینه بیشینه برای یک بازی دو نفره این است که راس های درخت به گونه ای ارزش ( امتیاز ) گذاری شوند که ارزش هر راس بیان گر میزان برتری بازکن نخست باشد. در این صورت:
- اگر در یک راس نوبت با بازیکن نخست باشد ارزش آن راس برابر است با بیش ترین ارزش نسبت داده شده به فرزندان آن ( به چنین راسی Max node یا راس بیشینه گفته می شود )
- اگر در یک راس نوبت با بازیکن دوم باشد ارزش آن راس برابر است با کم ترین ارزش نسبت داده شده به فرزندان آن ( به چنین راسی Min node یا راس کمینه گفته می شود )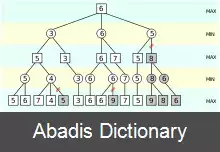
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای بررسی ایدهٔ کلی هرس آلفا بتا این دو مسئلهٔ مشابه را در نظر بگیرید:
- تعدادی زیر مجموعهٔ ناتهی و متناهی از مجموعهٔ اعداد حقیقی در اختیار داریم. ارزش ( یا امتیاز ) هر یک از این مجموعه ها را برابر با کوچک ترین عضو آن تعریف می کنیم. هدفمان یافتن مجموعه ای با بیش ترین ارزش است.
فرض کنید که ارزش یکی از مجموعه ها برابر با m است. در این صورت مجموعه ای که دست کم یک عضو کوچک تر از m داشته باشد، پاسخ مسئله نخواهد بود. پس نیازی به بررسی اعضای این مجموعه ( و یافتن ارزش آن ) نیست. ( چرا که ارزش آن کوچک تر از m است )
- همان پرسش بالا را این گونه تغییر می دهیم: ارزش هر مجموعه برابر با بزرگ ترین عضو آن تعریف می شود و هدف یافتن کم ارزش ترین مجموعه است.
در این حالت نیز اگر مجموعه ای با ارزش m وجود داشته باشد مجموعه هایی که حداقل یک عضو بزرگ تر از m دارند، نمی توانند پاسخ مسئله باشند.
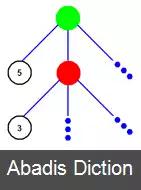
از همین ایده می توان برای بهینه کردن پیمایش روی درخت کمینه بیشینه بهره جست. شکل زیر را به عنوان بخشی از یک درخت کمینه بیشینه در نظر بگیرید:
فرض کنید ارزش ( امتیاز ) راس سبز را برابر با بیش ترین ارزش نسبت داده شده به فرزندان آن راس تعریف کنیم و ( مطابق با تعریف درخت کمینه بیشینه ) ارزش راس قرمز برابر با کم ترین ارزش نسبت داده شده به فرزندان آن راس تعریف شود. حال اگر هدف یافتن ارزش راس سبز باشد، نیازی به پیمایش زیر درخت راس قرمز و یافتن ارزش این راس نیست. چرا که ارزش راس قرمز حداکثر برابر ۳ می باشد در حالی که راس سبز فرزندی با ارزش ۵ دارد.
یکی از راه های پیاده سازی درخت کمینه بیشینه برای یک بازی دو نفره این است که راس های درخت به گونه ای ارزش ( امتیاز ) گذاری شوند که ارزش هر راس بیان گر میزان برتری بازکن نخست باشد. در این صورت:
- اگر در یک راس نوبت با بازیکن نخست باشد ارزش آن راس برابر است با بیش ترین ارزش نسبت داده شده به فرزندان آن ( به چنین راسی Max node یا راس بیشینه گفته می شود )
- اگر در یک راس نوبت با بازیکن دوم باشد ارزش آن راس برابر است با کم ترین ارزش نسبت داده شده به فرزندان آن ( به چنین راسی Min node یا راس کمینه گفته می شود )


wiki: هرس آلفا بتا
