در هندسهٔ تحلیلی، هذلولی گون ( به انگلیسی: Hyperboloid ) یک رویه و از انواع رویه های درجهٔ دوم است. [ ۱]
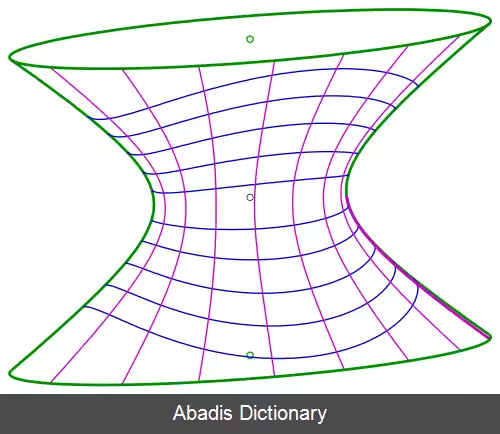
هذلولی گون دورانی حالت خاصی از هذلولی گون است که از دوران یک هذلولی حول محور تقارن آن به دست می آید.
هذلولی گون به دو دستهٔ یکپارچه ( همبند ) و هذلولی گون دوپارچه ( ناهمبند ) تقسیم می شود.
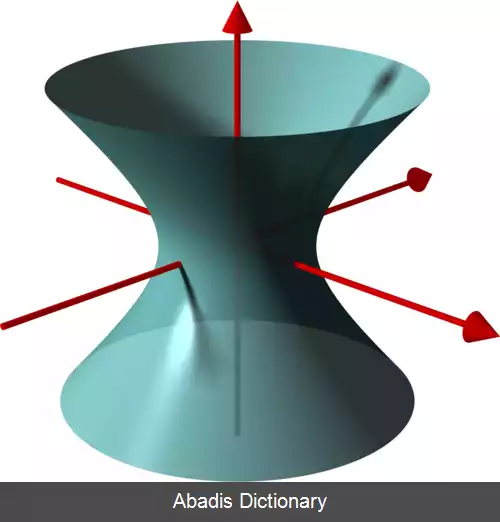
در دستگاه مختصات دکارتی، روش استاندارد نمایش یک هذلولی گون یکپارچه با مرکز تقارن در مبدأ مختصات به صورت زیر است:[ ۱]
x 2 a 2 + y 2 b 2 − z 2 c 2 = 1
اگر a = b باشد هذلولی گون دورانی حاصل می شود.
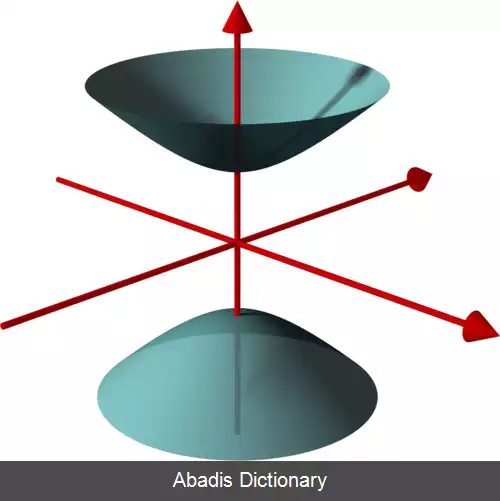
در دستگاه مختصات دکارتی، روش استاندارد نمایش یک هذلولی گون دوپارچه با مرکز تقارن در مبدأ مختصات به صورت زیر است:[ ۱]
x 2 a 2 + y 2 b 2 − z 2 c 2 = − 1
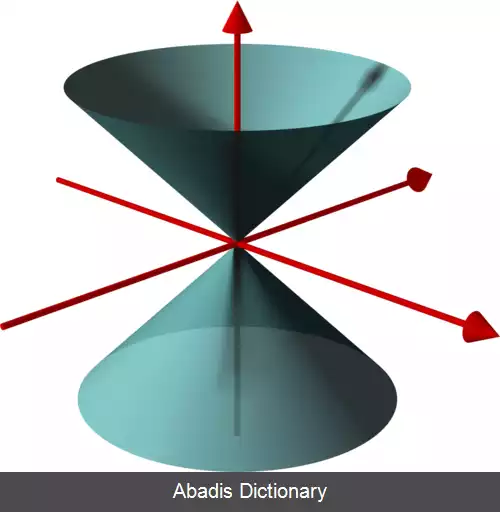
با این که سطح مخروطی هذلولی گون نیست، به دلیل شباهتش با هر دو نوع هذلولی گون آن را در این جا آوردیم:[ ۱]
x 2 a 2 + y 2 b 2 − z 2 c 2 = 0
اگر a = b باشد مخروط ( دایروی ) حاصل می شود.
یک ابرهذلولی گون در فضای R n ، یک ابررویهٔ درجه دو است. ابرهذلولی گون ممکن است چندپارچه باشد ( به این معنی که تعداد مؤلّفه های همبندی اش بیش از دو باشند ) .
یک ابرهذلولی گون، همهٔ نقاطی مانند P = ( x 1 , x 2 , … , x n ) است که در معادلهٔ استاندارد زیر صدق کنند:
± x 1 2 c 1 2 ± x 2 2 c 2 2 ± ⋯ ± x n 2 c n 2 = 1
هذلولی وارهای یکپارچه در معماری سازه ها استفاده می شوند، به این دلیل که می توان آن ها را با تیرآهن های راست ساخت که باعث کاهش هزینه ها و افزایش استحکام می شود.

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهذلولی گون دورانی حالت خاصی از هذلولی گون است که از دوران یک هذلولی حول محور تقارن آن به دست می آید.
هذلولی گون به دو دستهٔ یکپارچه ( همبند ) و هذلولی گون دوپارچه ( ناهمبند ) تقسیم می شود.
در دستگاه مختصات دکارتی، روش استاندارد نمایش یک هذلولی گون یکپارچه با مرکز تقارن در مبدأ مختصات به صورت زیر است:[ ۱]
x 2 a 2 + y 2 b 2 − z 2 c 2 = 1
اگر a = b باشد هذلولی گون دورانی حاصل می شود.
در دستگاه مختصات دکارتی، روش استاندارد نمایش یک هذلولی گون دوپارچه با مرکز تقارن در مبدأ مختصات به صورت زیر است:[ ۱]
x 2 a 2 + y 2 b 2 − z 2 c 2 = − 1
با این که سطح مخروطی هذلولی گون نیست، به دلیل شباهتش با هر دو نوع هذلولی گون آن را در این جا آوردیم:[ ۱]
x 2 a 2 + y 2 b 2 − z 2 c 2 = 0
اگر a = b باشد مخروط ( دایروی ) حاصل می شود.
یک ابرهذلولی گون در فضای R n ، یک ابررویهٔ درجه دو است. ابرهذلولی گون ممکن است چندپارچه باشد ( به این معنی که تعداد مؤلّفه های همبندی اش بیش از دو باشند ) .
یک ابرهذلولی گون، همهٔ نقاطی مانند P = ( x 1 , x 2 , … , x n ) است که در معادلهٔ استاندارد زیر صدق کنند:
± x 1 2 c 1 2 ± x 2 2 c 2 2 ± ⋯ ± x n 2 c n 2 = 1
هذلولی وارهای یکپارچه در معماری سازه ها استفاده می شوند، به این دلیل که می توان آن ها را با تیرآهن های راست ساخت که باعث کاهش هزینه ها و افزایش استحکام می شود.






wiki: هذلولی گون
