نیم گروه

در ریاضیات نیم گروه ( به انگلیسی: semigroup ) ساختاری جبریست که یک مجموعه مجهز به عمل دوتایی شرکت پذیر است.
عملیات دوتایی یک نیم گروه اغلب به صورت ضربی: x . y یا x y نوشته شده که نتیجه اعمال عمل نیم گروه به زوج مرتب ( x , y ) می باشد. شرکت پذیری را برای تمام x , y , z درون نیم گروه به صورت صوری ( x . y ) . z = x . ( y . z ) بیان می کنند.
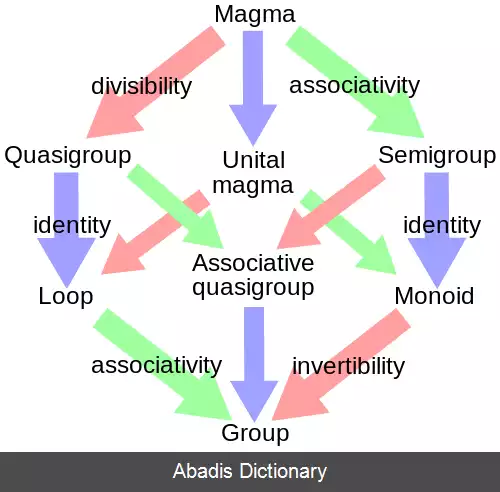
نیم گروه ها را می توان به عنوان حالت خاصی از ماگماها در نظر گرفت، که در آن عمل دوتایی شرکت پذیر است. یا می توان آن ها را به صورت تعمیمی از گروه ها بدون الزام به وجود عنصر معکوس پذیر در نظر گرفت. [ یادداشت ۱]
همچون گروه ها و ماگماها، عمل نیم گروه ها نیز لزوماً جابجایی نیستند، بنابر این x . y لزوماً برابر با y . x نیست؛ یک مثال شناخته شده از عملیاتی که شرکتپذیر است اما ناجابجایی است، عمل ضرب ماتریسی است. اگر عمل نیم گروه جابجایی باشد، آنگاه به نیم گروه مورد نظر، نیم گروه جابجایی گویند.
یک نیم گروه، مجموعه ای چون S با عمل دوتایی ". " ( یعنی تابعی چون . : S × S ← S ) است به گونه ای که در خاصیت شرکت پذیری صدق کند:
به طور خلاصه تر می توان گفت که نیم گروه یک ماگمای شرکت پذیر است.
↑ اصول موضوعه بستار با تعریف عمل دوتایی روی یک مجموعه به صورت خودکار اعمال می شود. لذا برخی از مؤلفان این الزام را حذف می کنند و سه اصول موضعه گروه و فقط یک اصل ( شرکت پذیری ) برای نیم گروه را ذکر می کنند.