نگاشت پوانکاره

در ریاضیات، به ویژه در سیستم های دینامیکی، نگاشت اولین بازگشت یا نگاشت پوانکاره، به نام آنری پوانکره، محل تلاقی یک مدار متناوب در فضای حالت یک سیستم دینامیکی پیوسته با یک زیرفضای بُعد - پایین تر معین، که بخش پوانکاره نامیده می شود، تراگری برای جریان سیستم است. به طور دقیق تر، می توان یک مدار متناوب را با شرایط اولیه درون بخشی از فضا در نظر گرفت، که پس از آن بخش را ترک می کند و نقطه ای را که این مدار برای اولین بار به بخش برمی گردد، مشاهده می کند. سپس یک نگاشت ایجاد می کند تا اولین نقطه را به نقطه دوم بفرستد، از این رو نام آن نگاشت اولین بازگشت است. تراگری بخش پوانکاره بدین معناست که مدارهای متناوب که از زیرفضای جریان شروع می شوند از آن عبور می کنند و نه موازی با آن. [ نیازمند منبع]
نگاشت پوانکاره را می توان به عنوان یک سیستم گسسته ی پویا با فضای حالت تعبیر کرد که یک بعد کوچک تر از سیستم دینامیکی پیوسته اصلی است. از آنجا که بسیاری از خصوصیات مدارهای متناوب و شبه متناوب سیستم اصلی را حفظ می کند و فضای حالت بعدی کمتری دارد، اغلب برای تجزیه و تحلیل سیستم اصلی به روشی ساده تر استفاده می شود. [ نیازمند منبع] در عمل این همیشه امکان پذیر نیست زیرا هیچ روش کلی برای ساختن نگاشت پوانکاره وجود ندارد.
یک نگاشت پوانکاره از یک طرح بازگشتی در آن فضا متفاوت است و زمان تعیین نمی کند که چه وقت یک نقطه ترسیم شود. به عنوان مثال، مکان ماه در اوج و حضیض زمین یک طرح بازگشتی است. مکان ماه هنگام عبور از صفحه عمود بر مدار زمین و عبور از خورشید و زمین در اوج و حضیض، یک نگاشت پوانکاره است[ نیازمند منبع] که توسط میشل هنون برای مطالعه حرکت ستاره ها در کهکشان استفاده شد، زیرا مسیر ستاره ای که به یک صفحه تصویر می شود مانند یک نابسامانی درهم پیچیده به نظر می رسد، در حالی که نگاشت پوانکاره ساختار را با وضوح بیشتری نشان می دهد.
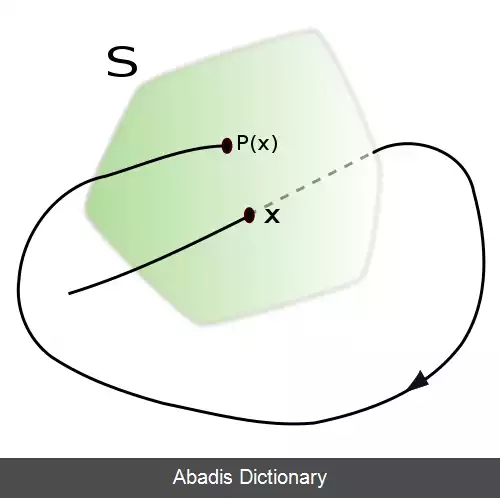
اگر ( R , M، φ ) یک سیستم دینامیکی عمومی، با R اعداد حقیقی، M فضای فاز و φ تابع تکامل باشد. اگر γ یک مدار متناوب از میان یک نقطه p و S یک بخش محلی و تراگری مشتق پذیر از φ گذرانده از p باشد، به آن بخش پوانکاره گذرانده از p می گویند.
با توجه به همسایگی باز و همبند U ⊂ S از p، یک تابع
برای مدار γ بر بخش پوانکاره S گذرانده ار نقطه p نگاشت پوانکاره گفته می شود.