نگاره فاز

نگاره فاز یا فیز پرتره نمایش هندسی مسیرهای یک سامانه پویا در صفحه فاز است. هر مجموعه از شرایط اولیه با یک منحنی یا نقطه متفاوت نشان داده می شود.
نگاره های فاز ابزاری ارزشمند در مطالعه سامانه های پویا هستند. آنها از یک رسم از سیرهای معمول در فضای حالت تشکیل شده اند. این اطلاعاتی از قبیل وجود جاذب، دافع یا چرخه حدی برای مقدار پارامتر انتخاب شده را نشان می دهد. مفهوم هم ارزی توپولوژیک در طبقه بندی رفتار سیستم ها با تعیین زمانی که دو نگاره فاز مختلف رفتار پویای کیفی یکسانی را نشان می دهند، مهم است. جاذب یک نقطه پایدار است که به آن «چاه» گفته می شود. دافع به عنوان یک نقطه ناپایدار در نظر گرفته می شود، که به عنوان «چشمه» نیز شناخته می شود.
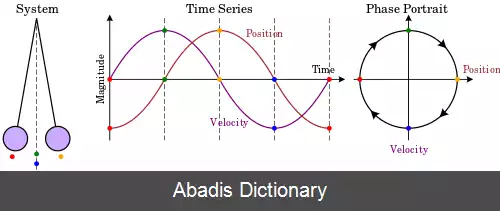
نمودار نگاره فاز یک سامانه پویا مسیرهای سامانه ( با فلش ) و حالت های ثابت پایدار ( با نقطه ) و حالت های ثابت ناپایدار ( با دایره ) را در یک فضای حالت به تصویر می کشد. محورها متغیرهای حالت هستند.
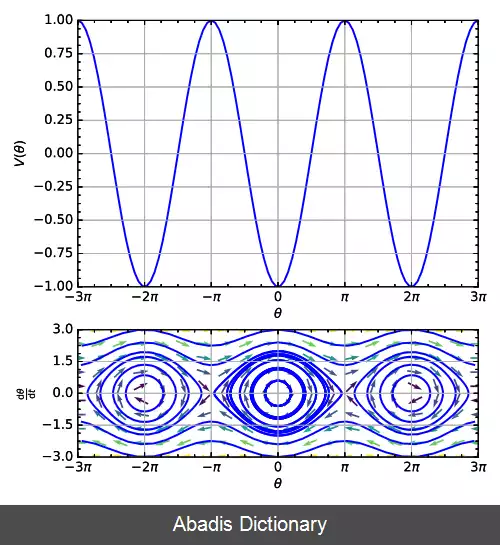
• آونگ ساده، به تصویر ( سمت راست ) مراجعه کنید.
• نوسان گر هارمونیکی ساده که در آن نگاره فاز از بیضی هایی تشکیل شده است که در مبدأ قرار دارند، که یک نقطه ثابت است.
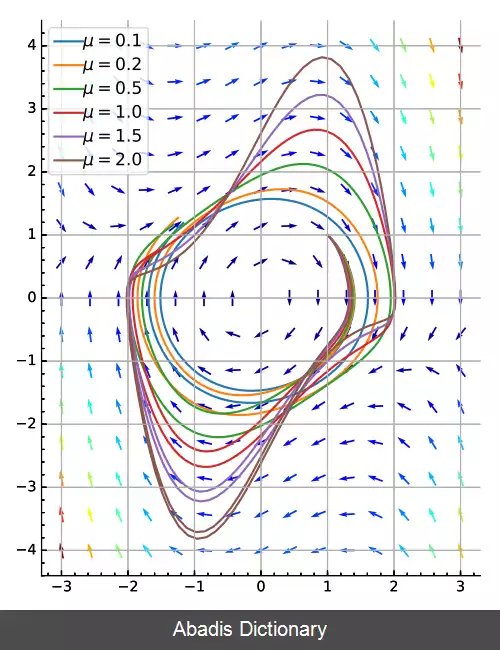
• نوسان ساز ون در پل تصویر ( پایین سمت راست ) را ببینید.
• صفحه پارامتر ( صفحه c ) و مجموعه ماندبلرو
نگاره فاز نشان دهنده رفتار جهت دار سیستم ODE است. نگاره فاز می تواند پایداری سیستم را نشان دهد. [ ۱]
رفتار نگاره فاز یک سیستم از ODEها را می توان با مقادیر ویژه یا رَد و دترمینان ( رَد λ 1 + λ 2 = ، دترمینان λ 1 × λ 2 = ) سیستم تعیین کرد. [ ۱]