نوسانگر هماهنگ کوانتومی، نام سیستمی است که از اعمال شرایط کوانتمی بر نوسانگر هماهنگ کلاسیکی بدست می آید. از آنجایی که یک پتانسیل دلخواه می تواند به صورت یک پتانسیل هماهنگ در همسایگی نقطه تعادل تقریب زده شود، این مدل از مهم ترین مدل های سامانه های کوانتومی است. هچنین این از معدود سامانه های کوانتمی است که برای آن جواب دقیق تحلیلی وجود دارد و نیازی به شبیه سازی عددی برای حل ندارد. [ ۱] [ ۲] [ ۳]
عملگر هامیلتونی ذره به صورت زیر است:
که m جرم ذره, ω فرکانس زاویه ای نوسانگر, ∧ x عملگر مکان ( = x ) , و ∧ p عملگر تکانه است:
اولین بخش از عملگر هامیلتونی بیانگر انرژی های جنبشی ممکن برای ذره است و دومین بخش بیانگر وضعیت های ممکن برای انرژی پتانسیل است. با فرض آنکه پتانسیل به زمان وابسته نیست می توان معادله شرودینگر مستقل از زمان را نوشت:
که E بیانگر انرژی است و با حل این معادله ویژه مقداری بدست خواهد آمد و این ویژه مقادیر این معادله است. |ψ⟩ بیانگر ویژه توابع این معادله است.
یکی از روش های حل این معادله مانند بسیاری از معادله های شرودینگر استفاده از روش های طیفی است که این پاسخ را می دهد.
که Hn چندجمله ای هرمیتی فیزیکی است:
ویژه مقادیر انرژی هم به صورت زیر است:
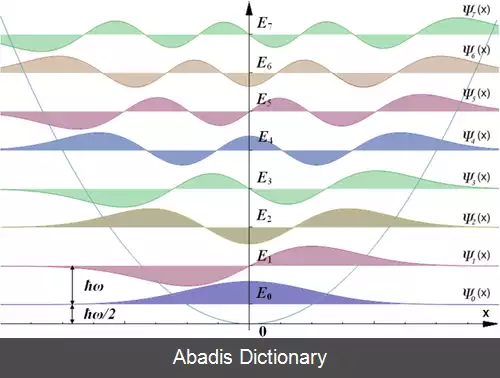
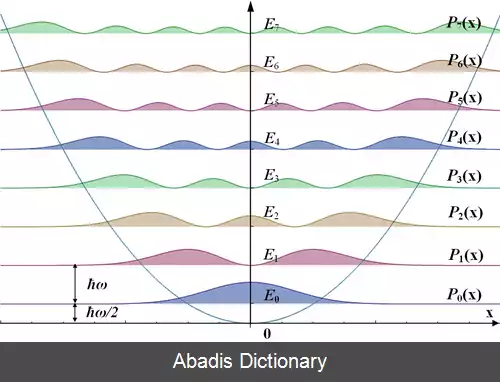
طیف انرژی به سه جهت قابل توجه است: اول اینکه انرژی گسسته است بدین معنی که فقط مقادیر خاصی ( ضرایب صحیح به علاوه نیم از ħω ) قابل قبول است. دوم اینکه این انرژی به طور یکسانی توزیع شده است برخلاف مدل بور یا ذره در جعبه. سوم اینکه کمترین انرژی ( انرژی حالت پایه؛ n = 0 ) برابر با پتانسیل چاه نیست بلکه به اندازه ħω/2 بالای آن است. چرا که ذرات در حالت پایه طبق اصل عدم قطعیت هایزنبرگ نباید انرژی صفر داشته باشند. انرژی نقطه صفر تاثیر مهمی در نظریه میدان های کوانتمی و گرانش کوانتمی دارد.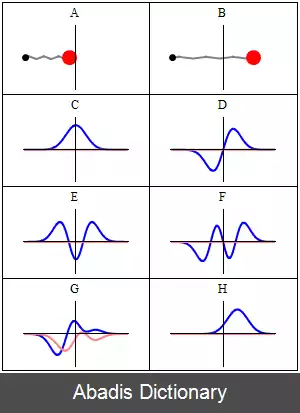
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفعملگر هامیلتونی ذره به صورت زیر است:
که m جرم ذره, ω فرکانس زاویه ای نوسانگر, ∧ x عملگر مکان ( = x ) , و ∧ p عملگر تکانه است:
اولین بخش از عملگر هامیلتونی بیانگر انرژی های جنبشی ممکن برای ذره است و دومین بخش بیانگر وضعیت های ممکن برای انرژی پتانسیل است. با فرض آنکه پتانسیل به زمان وابسته نیست می توان معادله شرودینگر مستقل از زمان را نوشت:
که E بیانگر انرژی است و با حل این معادله ویژه مقداری بدست خواهد آمد و این ویژه مقادیر این معادله است. |ψ⟩ بیانگر ویژه توابع این معادله است.
یکی از روش های حل این معادله مانند بسیاری از معادله های شرودینگر استفاده از روش های طیفی است که این پاسخ را می دهد.
که Hn چندجمله ای هرمیتی فیزیکی است:
ویژه مقادیر انرژی هم به صورت زیر است:
طیف انرژی به سه جهت قابل توجه است: اول اینکه انرژی گسسته است بدین معنی که فقط مقادیر خاصی ( ضرایب صحیح به علاوه نیم از ħω ) قابل قبول است. دوم اینکه این انرژی به طور یکسانی توزیع شده است برخلاف مدل بور یا ذره در جعبه. سوم اینکه کمترین انرژی ( انرژی حالت پایه؛ n = 0 ) برابر با پتانسیل چاه نیست بلکه به اندازه ħω/2 بالای آن است. چرا که ذرات در حالت پایه طبق اصل عدم قطعیت هایزنبرگ نباید انرژی صفر داشته باشند. انرژی نقطه صفر تاثیر مهمی در نظریه میدان های کوانتمی و گرانش کوانتمی دارد.



wiki: نوسانگر هماهنگ کوانتمی
