نوتروسوفی ( نام علمی: Neutrosophy ) شاخه جدیدی از فلسفه می باشد که به اصل، طبیعت و منظور خنثی ها و همچنین کنش های آن با تخیل ایده آلی می پردازد.
نوتروسوفیک ها توسط فلورنتین اسمارانداچ در سال ۱۹۹۵ معرفی شدند.
این نظریه شامل هر تصور یا ایده < A> را همراه با ضد آن یا < آنتی - A> و توهم "خنثی ها" < Neut - A> در نظر می گیرد ( به طور مثال تصورات یا ایده های واقع شده بین دو اکسترمم که نه با < A> و نه با < آنتی - A> تطابق دارند ) . ایده های < Neut - A> و < آنتی - A> با یکدیگر با عنوان < غیر - A> یاد می شوند.
مطابق این نظریه، هر ایده < A> گرایش به خنثی یا بالانس شدن با ایده های < آنتی - A> و < غیر - A> را، به عنوان حالت تعادل، خواهند داشت.
به روشی کلاسیکی، < A> ، < Neut - A> ، < آنتی - A> دو به دو مجزا هستند. ولی از آنجا که در بسیاری از حالات مرز بین تصورات مبهم و غیر دقیق هستند، ممکن است که < A> ، < Neut - A> ، < آنتی - A> ( و به طور بدیهی < غیر - A> ) دو به دو اجزاء مشترکی نیز داشته باشند.
نوتروسوفی، پایه منطق نوتروسوفیک، مجموعه نوتروسوفیک، احتمال نوتروسوفیک. استاتیک نوتروسوفیک مورد استفاده در مهندسی ( خصوصاً در ترکیب اطلاعات یا نرم افزار ) ، طب، ارتش، فیزیولوژی و فیزیک می باشد.
منطق نوتروسوفیک یک چارچوب عمومی برای وحدت بسیاری از منطق های موجود می باشد و منطق غیر شفاف را تعمیم می دهد ( خصوصاً منطق غیر شفاف شهودی را ) . ایده اصلی منطق نوتروسوفیک ( NL ) مشخص کردن هر عبارت منطقی در یک فضای سه بعدی نوتروسوفیک می باشد که در آن هر بعد فضا به ترتیب معرف درستی ( T ) ، غلط بودن ( F ) و عدم قطعیت ( I ) عبارت مورد نظر می باشد و در آن T، I و F زیرمجموعه های استاندارد یا غیراستاندارد ] - 0, 1+[ می باشند.
برای طرح های مهندسی نرم افزار بازه واحد کلاسیکی را می توان مورد استفاده قرار داد. T، I و F اجزاء مستقلی هستند، که جایی برای اطلاعات ناقص ( وقتی که جمع بالائی آنان < 1 باشد ) ، اطلاعات غیرسازگار و متناقض ( وقتی که جمع بالائی آنان > 1 باشد ) یا اطلاعات کامل ( مجموعه اجزاء مساوی 1 باشد ) باز می نمایند.
به عنوان یک مثال، یک عبارت می تواند بین و درست، {0. 1} یا بین ( 0. 15, 0. 25 ) و غیرقابل تعیین، یا 0. 4 یا 0. 6 و غلط باشد.
مجموعه نوتروسوفیک تعمیمی از مجموعه غیر شفاف می باشد ( خصوصاً مجموعه غیر شفاف شهودی ) . فرض کنید U یک عالم مباحثه باشد، و M یک مجموعه واقع در U باشد. یک جزء x از U نسبت به مجموعه M به صورت x ( T, I, F ) بیان می شود و به صورت زیر متعلق به M می باشد: t% درست در مجموعه است، i% غیرقابل تعیین ( یا ناشناخته ) در مجموعه است، و f% هم غیر درست در مجموعه است، که t در T تغییر می کند، I در I، و f در F. به طور استاتیکی، T، I و F زیرمجموعه هستند، ولی به طور دینامیکی T، I و F توابع/عملگر هستند ( بسته به بسیاری از پارامترهای شناخته شده و ناشناخته ) .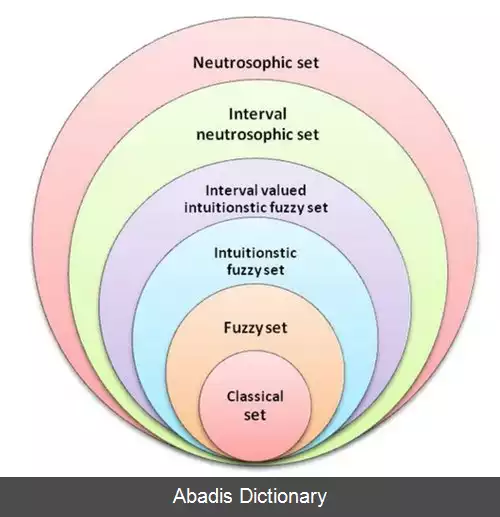
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنوتروسوفیک ها توسط فلورنتین اسمارانداچ در سال ۱۹۹۵ معرفی شدند.
این نظریه شامل هر تصور یا ایده < A> را همراه با ضد آن یا < آنتی - A> و توهم "خنثی ها" < Neut - A> در نظر می گیرد ( به طور مثال تصورات یا ایده های واقع شده بین دو اکسترمم که نه با < A> و نه با < آنتی - A> تطابق دارند ) . ایده های < Neut - A> و < آنتی - A> با یکدیگر با عنوان < غیر - A> یاد می شوند.
مطابق این نظریه، هر ایده < A> گرایش به خنثی یا بالانس شدن با ایده های < آنتی - A> و < غیر - A> را، به عنوان حالت تعادل، خواهند داشت.
به روشی کلاسیکی، < A> ، < Neut - A> ، < آنتی - A> دو به دو مجزا هستند. ولی از آنجا که در بسیاری از حالات مرز بین تصورات مبهم و غیر دقیق هستند، ممکن است که < A> ، < Neut - A> ، < آنتی - A> ( و به طور بدیهی < غیر - A> ) دو به دو اجزاء مشترکی نیز داشته باشند.
نوتروسوفی، پایه منطق نوتروسوفیک، مجموعه نوتروسوفیک، احتمال نوتروسوفیک. استاتیک نوتروسوفیک مورد استفاده در مهندسی ( خصوصاً در ترکیب اطلاعات یا نرم افزار ) ، طب، ارتش، فیزیولوژی و فیزیک می باشد.
منطق نوتروسوفیک یک چارچوب عمومی برای وحدت بسیاری از منطق های موجود می باشد و منطق غیر شفاف را تعمیم می دهد ( خصوصاً منطق غیر شفاف شهودی را ) . ایده اصلی منطق نوتروسوفیک ( NL ) مشخص کردن هر عبارت منطقی در یک فضای سه بعدی نوتروسوفیک می باشد که در آن هر بعد فضا به ترتیب معرف درستی ( T ) ، غلط بودن ( F ) و عدم قطعیت ( I ) عبارت مورد نظر می باشد و در آن T، I و F زیرمجموعه های استاندارد یا غیراستاندارد ] - 0, 1+[ می باشند.
برای طرح های مهندسی نرم افزار بازه واحد کلاسیکی را می توان مورد استفاده قرار داد. T، I و F اجزاء مستقلی هستند، که جایی برای اطلاعات ناقص ( وقتی که جمع بالائی آنان < 1 باشد ) ، اطلاعات غیرسازگار و متناقض ( وقتی که جمع بالائی آنان > 1 باشد ) یا اطلاعات کامل ( مجموعه اجزاء مساوی 1 باشد ) باز می نمایند.
به عنوان یک مثال، یک عبارت می تواند بین و درست، {0. 1} یا بین ( 0. 15, 0. 25 ) و غیرقابل تعیین، یا 0. 4 یا 0. 6 و غلط باشد.
مجموعه نوتروسوفیک تعمیمی از مجموعه غیر شفاف می باشد ( خصوصاً مجموعه غیر شفاف شهودی ) . فرض کنید U یک عالم مباحثه باشد، و M یک مجموعه واقع در U باشد. یک جزء x از U نسبت به مجموعه M به صورت x ( T, I, F ) بیان می شود و به صورت زیر متعلق به M می باشد: t% درست در مجموعه است، i% غیرقابل تعیین ( یا ناشناخته ) در مجموعه است، و f% هم غیر درست در مجموعه است، که t در T تغییر می کند، I در I، و f در F. به طور استاتیکی، T، I و F زیرمجموعه هستند، ولی به طور دینامیکی T، I و F توابع/عملگر هستند ( بسته به بسیاری از پارامترهای شناخته شده و ناشناخته ) .

wiki: نوتروسوفی
