نمودار نایکوئیست ( به انگلیسی: Nyquist plot ) نمودار پارامتری یک تابع تبدیل است که در سیستم های کنترل و پردازش سیگنال استفاده می شود. بیشترین استفاده ای که از این نمودار می شود، تشخیص پایداری سیستم های دارای فیدبک است. در محور افقی قسمت حقیقی تابع تبدیل رسم می شود و در محور عمودی قسمت موهومی آن رسم می شود. این نمودار بر حسب فرکانس رسم می شود. [ ۱]
در سال ۱۹۳۲ فردی به نام «نایکویست» از قضیه «کوشی» ( Cauchy ) استفاده کرد و در آن یک تابع از متغیرهای مختلط را در نظر گرفت تا به عنوان یک معیار در پایداری سیستم ها مورد استفاده قرار گیرد. قضیه کوشی مربوط به نگاشت «نواحی یا کانتورها» ( Contours ) از یک صفحه مختلط به صفحه ای دیگر است. به دلیل اینکه مطلوب است ریشه های معادله مشخصه در نیم صفحه راست محور jω قرار گیرد، ما کانتوری که کل نیم صفحه راست را احاطه می کند ( توسط تابع تبدیل سیستم ) نگاشت می دهیم. معادله مشخصه زیر را در نظر بگیرید:
1 + G H ( s ) = 0
این معادله مشخصه در واقع یک تابع F ( S ) از متغیر مختلط S است که برابر با صفر قرار داده شده باشد:
F ( S ) = 1 + G H ( S ) = 0
معادله فوق را می توان به صورت زیر در نظر گرفت:
F ( s ) = ÷
در این رابطه، ziها برابر با ریشه های معادله مشخصه و Pjها برابر با قطب های تابع تبدیل حلقه باز سیستم یا GH هستند. ما ابتدا کانتورهای صفحه S را به صفحه 1+GH نگاشت می کنیم. سپس برای سادگی از یک در 1+GH صرف نظر می کنیم و کانتورها را به صفحه GH نگاشت می کنیم. کانتورهایی که در این مرحله به دست می آیند، اطلاعاتی را درباره ریشه هایی به دست می دهند که دارای قسمت حقیقی مثبت هستند. در واقع، این ها همان ریشه هایی هستند که در صفحه سمت راست واقع شده اند.
قضیه کوشی قادر است که اطلاعاتی را درباره تعداد صفرهای مربوط به تابع F ( S ) فراهم کند که قسمت حقیقی مثبت دارند. در مورد بررسی پایداری یک سیستم، قضیه را باید به معادله مشخصه آن اعمال کرد که به صورت زیر نوشته می شود:
( 1 ) F ( S ) = 1 + G H ( S ) = 0
در این معادله F ( S ) معمولا به صورت زیر بیان می شود:
F ( s ) = ÷
حال اگر قضیه کوشی را به معادلات ۱ و ۲ اعمال کنیم، به صورت زیر خواهد بود.
اگر:
• یک کانتور در صفحه S را نگاشت کنیم که صفرهای Z و قطب های P مربوط به F ( S ) را محاصره کرده اند.
• کانتور از هیچ قطب یا صفر F ( S ) عبور نکند.
• جهت تراگشتی کانتورها در صفحه S ساعت گرد باشد.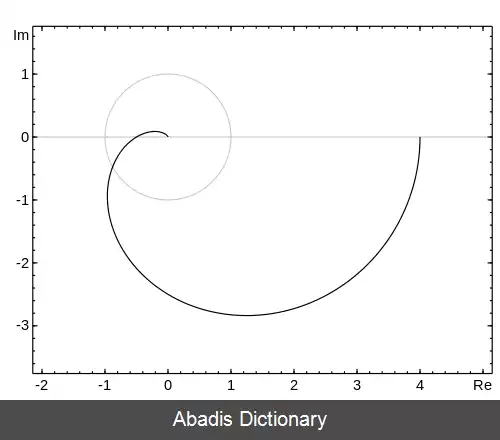
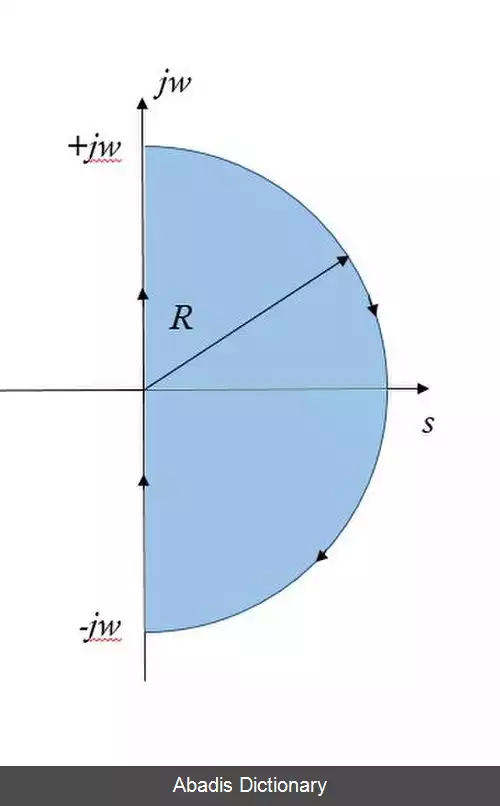
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر سال ۱۹۳۲ فردی به نام «نایکویست» از قضیه «کوشی» ( Cauchy ) استفاده کرد و در آن یک تابع از متغیرهای مختلط را در نظر گرفت تا به عنوان یک معیار در پایداری سیستم ها مورد استفاده قرار گیرد. قضیه کوشی مربوط به نگاشت «نواحی یا کانتورها» ( Contours ) از یک صفحه مختلط به صفحه ای دیگر است. به دلیل اینکه مطلوب است ریشه های معادله مشخصه در نیم صفحه راست محور jω قرار گیرد، ما کانتوری که کل نیم صفحه راست را احاطه می کند ( توسط تابع تبدیل سیستم ) نگاشت می دهیم. معادله مشخصه زیر را در نظر بگیرید:
1 + G H ( s ) = 0
این معادله مشخصه در واقع یک تابع F ( S ) از متغیر مختلط S است که برابر با صفر قرار داده شده باشد:
F ( S ) = 1 + G H ( S ) = 0
معادله فوق را می توان به صورت زیر در نظر گرفت:
F ( s ) = ÷
در این رابطه، ziها برابر با ریشه های معادله مشخصه و Pjها برابر با قطب های تابع تبدیل حلقه باز سیستم یا GH هستند. ما ابتدا کانتورهای صفحه S را به صفحه 1+GH نگاشت می کنیم. سپس برای سادگی از یک در 1+GH صرف نظر می کنیم و کانتورها را به صفحه GH نگاشت می کنیم. کانتورهایی که در این مرحله به دست می آیند، اطلاعاتی را درباره ریشه هایی به دست می دهند که دارای قسمت حقیقی مثبت هستند. در واقع، این ها همان ریشه هایی هستند که در صفحه سمت راست واقع شده اند.
قضیه کوشی قادر است که اطلاعاتی را درباره تعداد صفرهای مربوط به تابع F ( S ) فراهم کند که قسمت حقیقی مثبت دارند. در مورد بررسی پایداری یک سیستم، قضیه را باید به معادله مشخصه آن اعمال کرد که به صورت زیر نوشته می شود:
( 1 ) F ( S ) = 1 + G H ( S ) = 0
در این معادله F ( S ) معمولا به صورت زیر بیان می شود:
F ( s ) = ÷
حال اگر قضیه کوشی را به معادلات ۱ و ۲ اعمال کنیم، به صورت زیر خواهد بود.
اگر:
• یک کانتور در صفحه S را نگاشت کنیم که صفرهای Z و قطب های P مربوط به F ( S ) را محاصره کرده اند.
• کانتور از هیچ قطب یا صفر F ( S ) عبور نکند.
• جهت تراگشتی کانتورها در صفحه S ساعت گرد باشد.


wiki: نمودار نایکوئیست
