در هندسه، نماد هرمان - موگن برای نشان دادن عناصر تقارن در گروه های نقطه ای، گروه های صفحه و گروه های فضایی استفاده می شود. این نام از کریستالوگراف آلمانی کارل هرمان که آن را در سال ۱۹۲۸ میلادی معرفی کرد و کانی شناس فرانسوی چارلز ویکتور موگن که آن را در سال ۱۹۳۱ میلای اصلاح کرد گرفته شده است. این نماد گاهی اوقات نماد بین المللی نامیده می شود، زیرا به عنوان استاندارد توسط جداول بین المللی برای کریستالوگرافی از اولین ویرایش آنها در سال ۱۹۳۵ پذیرفته شد.
نماد هرمان موگن، در مقایسه با علامت گذاری شنفلیس، در کریستالوگرافی ترجیح داده می شود، زیرا می توان به راحتی از ان برای گنجاندن عناصر تقارن ترجمه استفاده کرد، و جهت محورهای تقارن را مشخص می کند.
محورهای چرخش با عدد n نشان داده می شوند - ۱، ۲، ۳، ۴، ۵، ۶، ۷، ۸ … ( زاویه چرخش φ = 360°/n ) . برای چرخش های نامناسب، نمادهای هرمان - موگن برخلاف علامت گذاری های شنفلیس و شوبنیکوف که محورهای چرخش - انعکاس را نشان می دهند محورهای روتووارونگی را نشان می دهد. محورهای روتووارون با عدد مربوط با یک ماکرون نشان داده می شوند، n — ۱, ۲, ۳, ۴, ۵, ۶, ۷, ۸, … . ۲ معادل یک صفحه آینه ای است و معمولاً به صورت m نشان داده می شود. جهت صفحه آینه به عنوان جهت عمود بر آن ( جهت ۲ محور ) تعریف می شود.
نمادهای هرمان موگان محورها و هواپیماهای غیر معادل را به صورت متقارن نشان می دهند. جهت یک عنصر تقارن با موقعیت آن در نماد هرمان - موگن مطابقت دارد. اگر یک محور چرخش n و یک صفحه آینه m یک جهت داشته باشند یعنی صفحه عمود بر محور باشد n، سپس آنها را به صورت کسری نشان می دهندn/m یا n / متر
اگر دو یا چند محور دارای جهت یکسان باشند، محور با تقارن بیشتر نشان داده می شود. تقارن بالاتر به این معنی است که محور الگویی با نقاط بیشتر ایجاد می کند. برای مثال، محورهای چرخشی ۳، ۴، ۵، ۶، ۷، ۸ به ترتیب الگوهای ۳ - ، ۴ - ، ۵ - ، ۶ - ، ۷ - ، ۸ نقطه ای ایجاد می کنند. محورهای چرخش نامناسب ۳، ۴، ۵، ۶، ۷، ۸ به ترتیب الگوهای ۶ - ، ۴ - ، ۱۰ - ، ۶ - ، ۱۴ - ، ۸ نقطه ای ایجاد می کنند. اگر یک چرخش و یک محور معکوس چرخشی تعداد نقاط یکسانی ایجاد کنند، باید محور چرخش انتخاب شود. برای مثال3/mترکیب ۶. از آنجایی که ۶ سبب ایجاد ۶ امتیاز می شود و ۳فقط ۳ ایجاد می کند، به جای آن باید ۶3/m ( نه۶/m، چون که ۶ قبلاً دارای صفحه آینه m بوده ) . به طور مشابه، در مواردی که هر دو ۳ و ۳ وجود دارد، ۳ نوشته شود. با این حال ما می نویسیم4/m، نه۴/m، چون هر دو ۴ و ۴ چهار نقطه ایجاد می کنند. در مورد6/m، که در آن ۲، ۳، ۶، ۳ و ۶ محور وجود دارد، محورهای ۳، ۶ و ۶ نیز همگی الگوهای ۶ نقطه ای ایجاد می کنند، ام به دلیل محور چرخشی بودن دومی استفاده می شود - نماد این کار را انجام می دهد. بودن6/m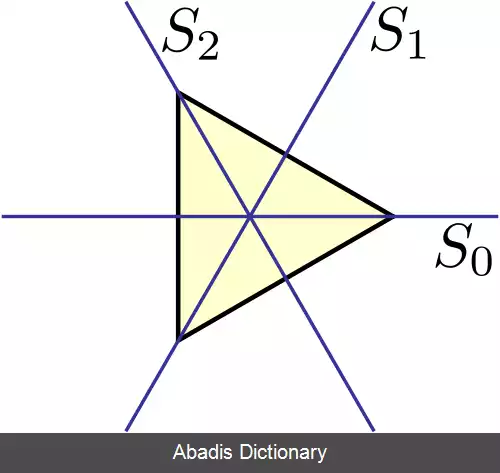
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنماد هرمان موگن، در مقایسه با علامت گذاری شنفلیس، در کریستالوگرافی ترجیح داده می شود، زیرا می توان به راحتی از ان برای گنجاندن عناصر تقارن ترجمه استفاده کرد، و جهت محورهای تقارن را مشخص می کند.
محورهای چرخش با عدد n نشان داده می شوند - ۱، ۲، ۳، ۴، ۵، ۶، ۷، ۸ … ( زاویه چرخش φ = 360°/n ) . برای چرخش های نامناسب، نمادهای هرمان - موگن برخلاف علامت گذاری های شنفلیس و شوبنیکوف که محورهای چرخش - انعکاس را نشان می دهند محورهای روتووارونگی را نشان می دهد. محورهای روتووارون با عدد مربوط با یک ماکرون نشان داده می شوند، n — ۱, ۲, ۳, ۴, ۵, ۶, ۷, ۸, … . ۲ معادل یک صفحه آینه ای است و معمولاً به صورت m نشان داده می شود. جهت صفحه آینه به عنوان جهت عمود بر آن ( جهت ۲ محور ) تعریف می شود.
نمادهای هرمان موگان محورها و هواپیماهای غیر معادل را به صورت متقارن نشان می دهند. جهت یک عنصر تقارن با موقعیت آن در نماد هرمان - موگن مطابقت دارد. اگر یک محور چرخش n و یک صفحه آینه m یک جهت داشته باشند یعنی صفحه عمود بر محور باشد n، سپس آنها را به صورت کسری نشان می دهندn/m یا n / متر
اگر دو یا چند محور دارای جهت یکسان باشند، محور با تقارن بیشتر نشان داده می شود. تقارن بالاتر به این معنی است که محور الگویی با نقاط بیشتر ایجاد می کند. برای مثال، محورهای چرخشی ۳، ۴، ۵، ۶، ۷، ۸ به ترتیب الگوهای ۳ - ، ۴ - ، ۵ - ، ۶ - ، ۷ - ، ۸ نقطه ای ایجاد می کنند. محورهای چرخش نامناسب ۳، ۴، ۵، ۶، ۷، ۸ به ترتیب الگوهای ۶ - ، ۴ - ، ۱۰ - ، ۶ - ، ۱۴ - ، ۸ نقطه ای ایجاد می کنند. اگر یک چرخش و یک محور معکوس چرخشی تعداد نقاط یکسانی ایجاد کنند، باید محور چرخش انتخاب شود. برای مثال3/mترکیب ۶. از آنجایی که ۶ سبب ایجاد ۶ امتیاز می شود و ۳فقط ۳ ایجاد می کند، به جای آن باید ۶3/m ( نه۶/m، چون که ۶ قبلاً دارای صفحه آینه m بوده ) . به طور مشابه، در مواردی که هر دو ۳ و ۳ وجود دارد، ۳ نوشته شود. با این حال ما می نویسیم4/m، نه۴/m، چون هر دو ۴ و ۴ چهار نقطه ایجاد می کنند. در مورد6/m، که در آن ۲، ۳، ۶، ۳ و ۶ محور وجود دارد، محورهای ۳، ۶ و ۶ نیز همگی الگوهای ۶ نقطه ای ایجاد می کنند، ام به دلیل محور چرخشی بودن دومی استفاده می شود - نماد این کار را انجام می دهد. بودن6/m


wiki: نماد هرمان موگن
