نماد لوی - چیویتا ( به انگلیسی: Levi - Civita symbol ) یا نماد جایگشت یک شبه تانسور همسانگرد است که برای ساده سازی در محاسبات تانسوری بسیار مفید است. این نماد به افتخار ریاضیدان ایتالیایی تولیو لوی - چیویتا ( به ایتالیایی: Tullio Levi - Civita ) نامگذاری شده است.
نماد لوی - چیویتا در سه بعد به صورت زیر تعریف می شود:
همچنین این نماد را می توان از رابطه زیر بدست آورد:
که % نماد عملگر باقی مانده است.
از این نماد مفید برای ساده سازی عبارات طولانی و پیچیده استفاده می شود. به عنوان مثال در ضرب خارجی a و b داریم:
که با استفاده از قرارداد جمع زنی انیشتین به صورت زیر در می آید:
و یا اگر A یک ماتریس ۳در۳ باشد، دترمینان آن را به صورت خلاصه زیر می توان نمایش داد:
این نماد را برای ابعاد دیگر هم می توان تعریف کرد. به این صورت که برای ε i j k l اگر i j k l . . . جایگشت زوجی از ( 1 , 2 , 3 , 4 , . . . ) باشد برابر + 1 و اگر جایگشت فردی از آن باشد برابر − 1 است. به عبارت دیگر: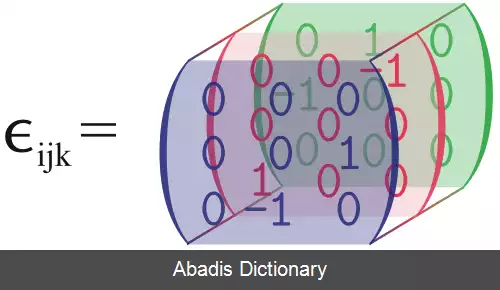
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنماد لوی - چیویتا در سه بعد به صورت زیر تعریف می شود:
همچنین این نماد را می توان از رابطه زیر بدست آورد:
که % نماد عملگر باقی مانده است.
از این نماد مفید برای ساده سازی عبارات طولانی و پیچیده استفاده می شود. به عنوان مثال در ضرب خارجی a و b داریم:
که با استفاده از قرارداد جمع زنی انیشتین به صورت زیر در می آید:
و یا اگر A یک ماتریس ۳در۳ باشد، دترمینان آن را به صورت خلاصه زیر می توان نمایش داد:
این نماد را برای ابعاد دیگر هم می توان تعریف کرد. به این صورت که برای ε i j k l اگر i j k l . . . جایگشت زوجی از ( 1 , 2 , 3 , 4 , . . . ) باشد برابر + 1 و اگر جایگشت فردی از آن باشد برابر − 1 است. به عبارت دیگر:

wiki: نماد لوی چیویتا
