مسئله نقطه در چندضلعی در هندسه محاسباتی مسئلهٔ تعیین قرارگیری یک نقطهٔ مشخص نسبت به یک چندضلعی داده شده است. یک نقطه می تواند داخل، خارج یا روی محیط چندضلعی قرار داشته باشد. این مسئله حالت خاص مسئلهٔ محل یابی نقطه است و در زمینه های پردازش اطلاعات گرافیکی، مانند گرافیک رایانه ای، بینایی رایانه ای، سامانه اطلاعات جغرافیایی، برنامه ریزی حرکت و طراحی رایانه ای کاربرد دارد.
ایوان سودرلند[ ۱] در سال ۱۹۷۴ دو راه حل ( انتشار پرتو و جمع زوایا ) برای این مسئله ارائه داد. تاریخچهٔ این مسئله و چند راه برد برای حل آن در یکی از شماره های مجلهٔ Ray Tracing News[ ۲] به چاپ رسیده است.
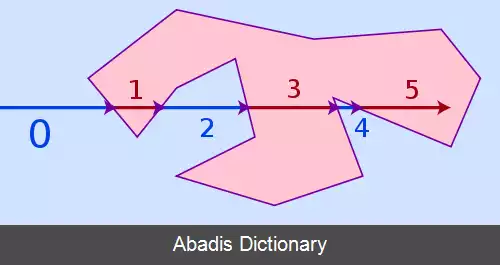
یک راه ساده برای آزمودن قرارگیری نقطه در داخل یک چندضلعی ساده، شمارش تعداد دفعات تقاطع یک پرتوی دلخواه با شروع از نقطهٔ مورد نظر با چندضلعی داده شده است. اگر نقطه داخل چندضلعی قرار داشته باشد، تعداد تقاطع ها فرد باشد نقطه داخل چندضلعی قرار دارد و اگر زوج باشد، نقطه خارج چندضلعی قرار دارد. از این الگوریتم با نام الگوریتم تعداد تقاطع یا الگوریتم قاعدهٔ زوج و فرد نیز یاد می شود و حداقل در سال ۱۹۶۲ کشف شده بوده است. [ ۳] این الگوریتم بر اساس این ایدهٔ ساده است که اگر یک نقطه از بی نهایت در جهت دلخواه حرکت کند و چندضلعی را چند بار قطع کند، در این صورت با هر بار قطع کردن چندضلعی به طور متناوب یک بار از بیرون چندضلعی به درون آن و یک بار از درون چندضلعی به بیرون آن جابجا می شود. در نتیجه با هر دو بار قطع کردن چندضلعی در همان سمت چندضلعی باقی می ماند. این مشاهده را می توان به طور ریاضیاتی توسط قضیهٔ خم جردن اثبات کرد.
اگر این الگوریتم در رایانه ای با ممیز_شناور پیاده سازی شود و نقطهٔ مورد نظر نزدیک مرز چندضلعی باشد، ممکن است این الگوریتم جواب نادرست دهد. البته این ایراد زیاد حائز توجه نیست، زیرا آن چه بیشتر مورد توجه است زمان اجرای الگوریتم است و نه صحت کامل الگوریتم. با این وجود برای اصلاح این مشکل، ثابت آنالیز_عددی رواداری_ ( مهندسی ) با نام ϵ تعریف می کنیم و قبل از اجرای الگوریتم بررسی می کنیم که اگر فاصلهٔ نقطه تا اضلاع چندضلعی کمتر از ϵ باشد، الگوریتم را متوقف کرده و نزدیک بودن بیش از اندازهٔ نقطه به اضلاع چندضلعی را گزارش می دهیم.
برای پیاده سازی این الگوریتم معمولاً به این صورت عمل می شود که وجود تقاطع بین پرتو و اضلاع متوالی چندضلعی بررسی می شوند. در چنین پیاده سازی ای باید به این مسئله توجه کرد که اگر پرتو از رأس_ ( هندسه ) مشترک دو ضلع چندضلعی عبور کند، آن گاه این تقاطع دو بار شمرده می شود. در مثال این بخش، این اتفاق در مورد بالاترین راس مشکلی ایجاد نمی کند ولی در مورد راست ترین راس، باعث بروز جواب نادرست خواهدشد. این مشکل را به این صورت برطرف می کنیم: اگر نقطهٔ تقاطع پرتو و یک ضلع، یکی از دو انتهای ضلع بود، در این صورت این تقاطع را تنها در صورتی شمارش می کنیم ( و فقط یک بار شمارش می کنیم ) که دو ضلع مجاور آن راس در دو طرف پرتو قرار گرفته باشند. این کار معادل این است که راس مورد نظر را اندکی به سمت بالای پرتو جابجا کرده باشیم.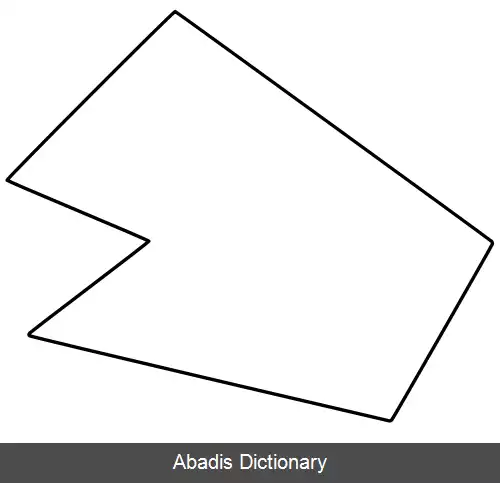
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفایوان سودرلند[ ۱] در سال ۱۹۷۴ دو راه حل ( انتشار پرتو و جمع زوایا ) برای این مسئله ارائه داد. تاریخچهٔ این مسئله و چند راه برد برای حل آن در یکی از شماره های مجلهٔ Ray Tracing News[ ۲] به چاپ رسیده است.
یک راه ساده برای آزمودن قرارگیری نقطه در داخل یک چندضلعی ساده، شمارش تعداد دفعات تقاطع یک پرتوی دلخواه با شروع از نقطهٔ مورد نظر با چندضلعی داده شده است. اگر نقطه داخل چندضلعی قرار داشته باشد، تعداد تقاطع ها فرد باشد نقطه داخل چندضلعی قرار دارد و اگر زوج باشد، نقطه خارج چندضلعی قرار دارد. از این الگوریتم با نام الگوریتم تعداد تقاطع یا الگوریتم قاعدهٔ زوج و فرد نیز یاد می شود و حداقل در سال ۱۹۶۲ کشف شده بوده است. [ ۳] این الگوریتم بر اساس این ایدهٔ ساده است که اگر یک نقطه از بی نهایت در جهت دلخواه حرکت کند و چندضلعی را چند بار قطع کند، در این صورت با هر بار قطع کردن چندضلعی به طور متناوب یک بار از بیرون چندضلعی به درون آن و یک بار از درون چندضلعی به بیرون آن جابجا می شود. در نتیجه با هر دو بار قطع کردن چندضلعی در همان سمت چندضلعی باقی می ماند. این مشاهده را می توان به طور ریاضیاتی توسط قضیهٔ خم جردن اثبات کرد.
اگر این الگوریتم در رایانه ای با ممیز_شناور پیاده سازی شود و نقطهٔ مورد نظر نزدیک مرز چندضلعی باشد، ممکن است این الگوریتم جواب نادرست دهد. البته این ایراد زیاد حائز توجه نیست، زیرا آن چه بیشتر مورد توجه است زمان اجرای الگوریتم است و نه صحت کامل الگوریتم. با این وجود برای اصلاح این مشکل، ثابت آنالیز_عددی رواداری_ ( مهندسی ) با نام ϵ تعریف می کنیم و قبل از اجرای الگوریتم بررسی می کنیم که اگر فاصلهٔ نقطه تا اضلاع چندضلعی کمتر از ϵ باشد، الگوریتم را متوقف کرده و نزدیک بودن بیش از اندازهٔ نقطه به اضلاع چندضلعی را گزارش می دهیم.
برای پیاده سازی این الگوریتم معمولاً به این صورت عمل می شود که وجود تقاطع بین پرتو و اضلاع متوالی چندضلعی بررسی می شوند. در چنین پیاده سازی ای باید به این مسئله توجه کرد که اگر پرتو از رأس_ ( هندسه ) مشترک دو ضلع چندضلعی عبور کند، آن گاه این تقاطع دو بار شمرده می شود. در مثال این بخش، این اتفاق در مورد بالاترین راس مشکلی ایجاد نمی کند ولی در مورد راست ترین راس، باعث بروز جواب نادرست خواهدشد. این مشکل را به این صورت برطرف می کنیم: اگر نقطهٔ تقاطع پرتو و یک ضلع، یکی از دو انتهای ضلع بود، در این صورت این تقاطع را تنها در صورتی شمارش می کنیم ( و فقط یک بار شمارش می کنیم ) که دو ضلع مجاور آن راس در دو طرف پرتو قرار گرفته باشند. این کار معادل این است که راس مورد نظر را اندکی به سمت بالای پرتو جابجا کرده باشیم.


wiki: نقطه در چندضلعی
