در حوزهٔ ریاضیات و در موضوع نظریه گراف، نظریهٔ کیرشهف یا نظریهٔ ماتریس درخت کیرشهف که از روی اسم گوستاو کیرشهف نامگذاری شده است در مود تعداد درخت های پوشا در یک گراف است که نشان می دهد این عدد را می توان در زمان چند جمله ای به عنوان دترمینان ماتریس به دست آمده از گراف محاسبه کرد. این نظریه یک تعمیم از فرمول کیلی است که تعداد درخت های پوشا در یک گراف کامل به دست می آورد.
نظریهٔ کیرشهف بر پایهٔ مفهموم ماتریس لاپلاس یک گراف است که برابر با اختلاف بین ماتریس درجه ( یک ماتریس قطری با درجهٔ راس ها در قطرها ) و ماتریس مجاورت آن است.
برای یک گراف همبند مشخص G با n راس نامگذاری شده فرض کنید λ1, λ2, … , λn−1 مقادیر ویژه غیر صفر ماتریس لاپلاس آن باشد. پس تعداد درخت های پوشای G برابر است با:
که یعنی تعداد درخت های پوشا برابر با هر هم عامل ماتریس لاپلاس G است.
در ابتدا، ماتریس لاپلاس Q را برای گراف الماسی G می نویسیم ( تصویر را در سمت چپ ببینید ) :
سپس، ماتریس * Q را با حذف کردن یکی از سطرها و ستون های ماتریس Q تشکیل می دهیم. برای مثال، با حذف ردیف ۱ و ستون ۱ داریم:
در نهایت، دترمینان * Q را برای ساخت ( t ( G به دست می آوریم که برای گراف الماسی برابر ۸ است. ( توجه کنید که ( t ( G یک هم عامل ( ۱٬۱ ) از Q در این مثال است )
ابتدا در نظر داشته باشید که لاپلاس خاصیتی دارد که مجموع تعداد مقادیرش در هر ستون و در هر ردیف برابر با صفر است. پس می توانیم هر کهاد را با افزودن ستون ها و ردیف ها، جابه جا کردن آن ها یا ضرب یک ردیف یا ستون در ۱ - یه یک کهاد دیگر تبدیل کنیم؛ بنابراین هم عامل ها مشابه هم هستند و می توان تأیید کرد که در واقع آن ها علامت یکسانی دارند.
در ادامه اقدام به نشان دادن این می کنیم که دترمینان کهاد M11 تعداد درخت های پوشا را می شمارد. فرض کنید n تعدا راس های گراف و m تعداد یال های آن باشد. ماتریس وقوع E یک ماتریس n در m است که به این صورت تعریف می شود: فرض کنید که ( i, j ) یال k - ام گراف باشد، و i < j. پس Eik = ۱ و Ejk = −۱، و تمام مقادیر ستون k برابر ۰ است. برای مثال قبل ( با n = ۴ و m = ۵ ) داریم:
در نظر داشته باشید که لاپلاس L می تواند به حاصل ضرب ماتریس وقوع و ترانهاده اش ساده شود، یعنی L = EET. علاوه بر این، فرض کنید F همان ماتریس E باشد که اولین ردیفش حذف شده باشد، پس داریم FFT = M11.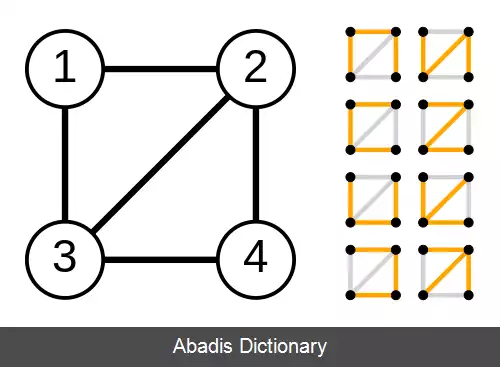
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنظریهٔ کیرشهف بر پایهٔ مفهموم ماتریس لاپلاس یک گراف است که برابر با اختلاف بین ماتریس درجه ( یک ماتریس قطری با درجهٔ راس ها در قطرها ) و ماتریس مجاورت آن است.
برای یک گراف همبند مشخص G با n راس نامگذاری شده فرض کنید λ1, λ2, … , λn−1 مقادیر ویژه غیر صفر ماتریس لاپلاس آن باشد. پس تعداد درخت های پوشای G برابر است با:
که یعنی تعداد درخت های پوشا برابر با هر هم عامل ماتریس لاپلاس G است.
در ابتدا، ماتریس لاپلاس Q را برای گراف الماسی G می نویسیم ( تصویر را در سمت چپ ببینید ) :
سپس، ماتریس * Q را با حذف کردن یکی از سطرها و ستون های ماتریس Q تشکیل می دهیم. برای مثال، با حذف ردیف ۱ و ستون ۱ داریم:
در نهایت، دترمینان * Q را برای ساخت ( t ( G به دست می آوریم که برای گراف الماسی برابر ۸ است. ( توجه کنید که ( t ( G یک هم عامل ( ۱٬۱ ) از Q در این مثال است )
ابتدا در نظر داشته باشید که لاپلاس خاصیتی دارد که مجموع تعداد مقادیرش در هر ستون و در هر ردیف برابر با صفر است. پس می توانیم هر کهاد را با افزودن ستون ها و ردیف ها، جابه جا کردن آن ها یا ضرب یک ردیف یا ستون در ۱ - یه یک کهاد دیگر تبدیل کنیم؛ بنابراین هم عامل ها مشابه هم هستند و می توان تأیید کرد که در واقع آن ها علامت یکسانی دارند.
در ادامه اقدام به نشان دادن این می کنیم که دترمینان کهاد M11 تعداد درخت های پوشا را می شمارد. فرض کنید n تعدا راس های گراف و m تعداد یال های آن باشد. ماتریس وقوع E یک ماتریس n در m است که به این صورت تعریف می شود: فرض کنید که ( i, j ) یال k - ام گراف باشد، و i < j. پس Eik = ۱ و Ejk = −۱، و تمام مقادیر ستون k برابر ۰ است. برای مثال قبل ( با n = ۴ و m = ۵ ) داریم:
در نظر داشته باشید که لاپلاس L می تواند به حاصل ضرب ماتریس وقوع و ترانهاده اش ساده شود، یعنی L = EET. علاوه بر این، فرض کنید F همان ماتریس E باشد که اولین ردیفش حذف شده باشد، پس داریم FFT = M11.

wiki: نظریه کیرشهف
