نظریه نرخ - اِعوِجاج ( نرخِ اعوجاج خوانده نشود ) ، یک شاخه اصلی از نظریه اطلاعات است که اصول نظری برای فشرده سازیِ خطادارِ داده ( دیتا ) است. این نظریه سعی در حل مسئلهٔ مشخص کردن حداقل تعداد بیت برای هر سمبل است ( که با نرخ R اندازه گرفته می شود ) که باید در کانال انتقال یابد به گونه ای که منبع اولیه را بتوان به صورت تقریبی در مقصد بازیابی کرد، ضمن اینکه اعوجاج ( Distortion ) از حد معینی ( D ) بیشتر نشود.
نظریه نرخ - اعوجاج یک فرمول بندی ریاضی است که بیان می کند چه مقدار فشرده سازیِ خطا دار امکان پذیر است. بسیاری از روش های فشرده سازی، صدا، گفتار، تصویر ثابت یا متحرک، دارای تبدیلات، کوانتیزاسیون، و روندهایی برای تعیین نرخ بیت هستند که در قالب کلی توابع نرخ - اعوجاج قرار می گیرند.
نظریه نرخ - اعوجاج توسط شانون در کار اساسی اش در نظریه اطلاعات شکل گرفت.
در نظریه نرخ - اعوجاج، معمولاً نرخ به عنوان تعداد بیت مورد استفاده برای هر سمبل به منظور ارسال یا فشرده سازی شناخته می شود. در بسیاری از موارد ساده، اعوجاج به صورت متوسطِ ( امیدِ ریاضی ) مربع اختلاف سیگنال ورودی و خروجی تعریف می شود. اما، از آنجایی که تکنیک های فشرده سازی خطادار روی داده هایی اعمال می شوند که قرار است برای انسان قابل درک باشند ( مانند موسیقی، تصاویر ثابت یا متحرک ) ، اندازه گیری اعوجاج باید به گونه ای مدل شود که متناسب با درک انسان باشد. بسیار شبیه استفاده از احتمالات در فشرده سازی خطا دار، معیارهای اعوجاج می توانند با توابع هزینه ( همان گونه که در تخمین بِیزَین و تئوری تصمیم استفاده می شود ) ، بیان شوند. در فشرده سازی صوت، مدل های ادراکی ( و در نتیجه اعوجاج ادراکی ) نسبتاً خوب پیشرفت کرده اند و به صورت معمول در تکنیک های فشرده سازی نظیر MP3 یا Vorbis استفاده می شوند، اما اغلب ساده نیست که در غالب تئوری نرخ - اعوجاج آورده شوند. در فشرده سازی تصویر ثابت یا متحرک، مدل های مبتنی بر ادراک انسان کمتر توسعه یافته اند و به صورت محدود در ماتریس وزن های JPEG و MPEG استفاده می شود.
توابعی که نرخ و اعوجاج را به هم مرتبط می کنند، جواب های مسئلهٔ کمینه سازی زیر هستند:
inf Q Y | X ( y | x ) I Q ( Y ; X ) subject to D Q ≤ D ∗ .
در اینجا ( QY | X ( y | x، که گاهی تست کانال نامیده می شود، تابع چگالی احتمال شرطی ( PDF ) خروجی کانال ارتباطی Y برای یک ورودی مفروض X است و ( IQ ( Y ; X اطلاعات متقابل بین Y و X است که به صورت زیر تعریف می شود: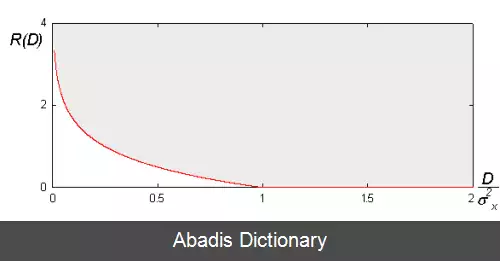
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنظریه نرخ - اعوجاج یک فرمول بندی ریاضی است که بیان می کند چه مقدار فشرده سازیِ خطا دار امکان پذیر است. بسیاری از روش های فشرده سازی، صدا، گفتار، تصویر ثابت یا متحرک، دارای تبدیلات، کوانتیزاسیون، و روندهایی برای تعیین نرخ بیت هستند که در قالب کلی توابع نرخ - اعوجاج قرار می گیرند.
نظریه نرخ - اعوجاج توسط شانون در کار اساسی اش در نظریه اطلاعات شکل گرفت.
در نظریه نرخ - اعوجاج، معمولاً نرخ به عنوان تعداد بیت مورد استفاده برای هر سمبل به منظور ارسال یا فشرده سازی شناخته می شود. در بسیاری از موارد ساده، اعوجاج به صورت متوسطِ ( امیدِ ریاضی ) مربع اختلاف سیگنال ورودی و خروجی تعریف می شود. اما، از آنجایی که تکنیک های فشرده سازی خطادار روی داده هایی اعمال می شوند که قرار است برای انسان قابل درک باشند ( مانند موسیقی، تصاویر ثابت یا متحرک ) ، اندازه گیری اعوجاج باید به گونه ای مدل شود که متناسب با درک انسان باشد. بسیار شبیه استفاده از احتمالات در فشرده سازی خطا دار، معیارهای اعوجاج می توانند با توابع هزینه ( همان گونه که در تخمین بِیزَین و تئوری تصمیم استفاده می شود ) ، بیان شوند. در فشرده سازی صوت، مدل های ادراکی ( و در نتیجه اعوجاج ادراکی ) نسبتاً خوب پیشرفت کرده اند و به صورت معمول در تکنیک های فشرده سازی نظیر MP3 یا Vorbis استفاده می شوند، اما اغلب ساده نیست که در غالب تئوری نرخ - اعوجاج آورده شوند. در فشرده سازی تصویر ثابت یا متحرک، مدل های مبتنی بر ادراک انسان کمتر توسعه یافته اند و به صورت محدود در ماتریس وزن های JPEG و MPEG استفاده می شود.
توابعی که نرخ و اعوجاج را به هم مرتبط می کنند، جواب های مسئلهٔ کمینه سازی زیر هستند:
inf Q Y | X ( y | x ) I Q ( Y ; X ) subject to D Q ≤ D ∗ .
در اینجا ( QY | X ( y | x، که گاهی تست کانال نامیده می شود، تابع چگالی احتمال شرطی ( PDF ) خروجی کانال ارتباطی Y برای یک ورودی مفروض X است و ( IQ ( Y ; X اطلاعات متقابل بین Y و X است که به صورت زیر تعریف می شود:

wiki: نظریه نرخ اعوجاج
