در حوزهٔ نظریه گراف، نردبان موبیوس Mnیک گراف دورانی مکعبی با تعداد رئوس زوج nاست، که از یک n - دور و چند یال
، تشکیل شده است. این گراف به این دلیل که دقیقاً n/2تا ۴ - دور ( McSorley 1998 ) دارد که به وسیله یال های مشترکشان به هم متصل اند و یک نوار موبیوس توپولوژیکی تشکیل می دهند، این گونه نام گذاری شده است. نردبان موبیوس اولین بار به وسیلهٔ Guy وHarary مورد مطالعه قرار گرفت و نام گذاری شد.
هر نردبان موبیوس غیر مسطح است. نردبان موبیوس دارای عدد تقاطع ۱ است، و می تواند در یک چنبره یا صفحهٔ مسطح جاسازی شود؛ بنابراین نردبان موبیوس نمونه ای از گراف های چنبره ای است. ( Li ( 2005 قابلیت جاسازی آن ها را در سطوح دستهٔ بالاتر کشف کرد. نردبانهای موبیوس رأس - ترایا ( vertex - transitive ) ( به استثناء ( M6 ) ) هستند نه یال - ترایا ( edge - transitive ) :هر رأس از دوری که نردبان از آن تشکیل شده است، مربوط به یک ۴ - دور است، در حالی که هر پله مربوط به دو تا از این دورها است. وقتی ( Mn, n ≡ 2 ( mod ۴دو قسمتی است. وقتی ( n ≡ 0 ( mod ۴با توجه به قضیهٔ بروکس ( Brooks' theorem ) دارای عدد رنگی ۳ است. ( De Mier, Noy ( 2005 نشان دادند که نردبان های موبیوس به وسیلهٔ تعدادحالات رنگ آمیزی با حد اقل رنگ ( chromatic polynomials ) مشخص می شوند. نردبان موبیوس M8دارای ۳۹۲ درخت پوشا است، این گراف و گراف M6بیشترین تعداد درختان پوشا را بین تمام گراف های مکعبی با تعداد رئوس مشابه، دارا هستند. ( Jakobson and Rivin 1999; Valdes 1991 ) با این حال، گراف ۱۰ رأسی با بیشترین درخت پوشا، گراف پترسن است، که نردبان موبیوس نیست.
نردبان موبیوس نقش مهمی در نظریه مینورهای گراف بازی می کند. آخرین نتیجه از این دست، قضیه ای از Klaus Wagner در ۱۹۳۷ بود که گراف هایی که مینور K5ندارند، می توانند با استفاده از عملیات clique - sumبرای ترکیب گراف های مسطح و نردبان موبیوسM8 ساخته شوند؛ به همین دلیل M8 گاهی گراف واگنر نامیده می شود.
( Gubser ( 1996 ) گراف تقریباً - مسطح را گرافی غیر مسطح که مینورهای مسطح دارد، تعریف کرد، او نشان داد که گرافهای ۳ - همبند تقریباً - مسطح یا نردبان های موبیوس هستند یا عضو تعداد کمی از سایر انواع، و سایر گرافهای تقریباً - مسطح را می توان با انجام عملیات ساده روی این گرافها ساخت.
( Maharry ( 2001نشان داد که تقریباً تمام گراف هایی که مینور مکعب ندارند می توانند با استفاده از عملیات ساده از نردبان موبیوس مشتاق شوند.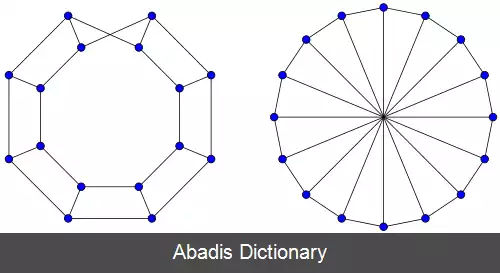
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف، تشکیل شده است. این گراف به این دلیل که دقیقاً n/2تا ۴ - دور ( McSorley 1998 ) دارد که به وسیله یال های مشترکشان به هم متصل اند و یک نوار موبیوس توپولوژیکی تشکیل می دهند، این گونه نام گذاری شده است. نردبان موبیوس اولین بار به وسیلهٔ Guy وHarary مورد مطالعه قرار گرفت و نام گذاری شد.
هر نردبان موبیوس غیر مسطح است. نردبان موبیوس دارای عدد تقاطع ۱ است، و می تواند در یک چنبره یا صفحهٔ مسطح جاسازی شود؛ بنابراین نردبان موبیوس نمونه ای از گراف های چنبره ای است. ( Li ( 2005 قابلیت جاسازی آن ها را در سطوح دستهٔ بالاتر کشف کرد. نردبانهای موبیوس رأس - ترایا ( vertex - transitive ) ( به استثناء ( M6 ) ) هستند نه یال - ترایا ( edge - transitive ) :هر رأس از دوری که نردبان از آن تشکیل شده است، مربوط به یک ۴ - دور است، در حالی که هر پله مربوط به دو تا از این دورها است. وقتی ( Mn, n ≡ 2 ( mod ۴دو قسمتی است. وقتی ( n ≡ 0 ( mod ۴با توجه به قضیهٔ بروکس ( Brooks' theorem ) دارای عدد رنگی ۳ است. ( De Mier, Noy ( 2005 نشان دادند که نردبان های موبیوس به وسیلهٔ تعدادحالات رنگ آمیزی با حد اقل رنگ ( chromatic polynomials ) مشخص می شوند. نردبان موبیوس M8دارای ۳۹۲ درخت پوشا است، این گراف و گراف M6بیشترین تعداد درختان پوشا را بین تمام گراف های مکعبی با تعداد رئوس مشابه، دارا هستند. ( Jakobson and Rivin 1999; Valdes 1991 ) با این حال، گراف ۱۰ رأسی با بیشترین درخت پوشا، گراف پترسن است، که نردبان موبیوس نیست.
نردبان موبیوس نقش مهمی در نظریه مینورهای گراف بازی می کند. آخرین نتیجه از این دست، قضیه ای از Klaus Wagner در ۱۹۳۷ بود که گراف هایی که مینور K5ندارند، می توانند با استفاده از عملیات clique - sumبرای ترکیب گراف های مسطح و نردبان موبیوسM8 ساخته شوند؛ به همین دلیل M8 گاهی گراف واگنر نامیده می شود.
( Gubser ( 1996 ) گراف تقریباً - مسطح را گرافی غیر مسطح که مینورهای مسطح دارد، تعریف کرد، او نشان داد که گرافهای ۳ - همبند تقریباً - مسطح یا نردبان های موبیوس هستند یا عضو تعداد کمی از سایر انواع، و سایر گرافهای تقریباً - مسطح را می توان با انجام عملیات ساده روی این گرافها ساخت.
( Maharry ( 2001نشان داد که تقریباً تمام گراف هایی که مینور مکعب ندارند می توانند با استفاده از عملیات ساده از نردبان موبیوس مشتاق شوند.

wiki: نردبان موبیوس
