در آنالیز عددی، نرخ همگرایی را سرعتِ همگرایی یک دنباله به حد خود تعریف می کنند. منظور از «حد دنباله» مقداری است که دنباله در بی نهایت به آن همگرا می شود. ( توجه کنید که لزوماً این مقدار وجود ندارد و می تواند حد یک دنباله بی نهایت باشد ( همانند دنباله رو به رو: a n = n 2 ) که در اینصورت اصطلاح نرخ «واگرایی» در عوض نرخ «همگرایی» برای آن تعریف می گردد ) . همان طور که ذکر شود نرخ همگرایی توسط حد دنباله تعیین می گردد و از آنجا که حد دنباله اطلاعاتی راجع به جملات اولیهٔ دنباله ( هر تعدادِ محدودی از اعضای ابتدای دنباله ) به ما نمی دهد لذا «نرخ همگرایی» و «حد» هیچ کدام هیچ اطلاعی راجع به ابتدای دنباله به ما نمی دهند و هر دو مفاهیمی برای کاوشِ رفتار دنباله در بی نهایت اند.
مفهوم نرخ همگرایی در هنگام کارکردن با برخی دنباله ها از اهمیت ویژه ای برخوردار است، برای مثال دنباله تقریباً اعشاری ( دنبالهٔ تقریبات یک عدد ( مثلاً A ) دنباله ای است که اعضای دنباله رفته رفته به عدد مدنظر ( A ) نزدیک تر می شوند و این نزدیکی عموماً به این صورت است که جمله بعدی نسبت به جمله قبلی یک دهم دقت بیشتر دارد، به عنوان مثال درادامه دنباله تقریبات عدد پی ( π ) آورده شده است: a 1 = 3 , a 2 = 3. 1 , a 3 = 3. 14 , . . . . همان طور که مطرح گردید نرخ همگرایی برای بررسی دنباله تقریباتی که از یک روش تکراری محاسبه ای ( iterative ) همانند گاوس سیدل ( یا هر روش موفق همگرایِ تکراری دیگری ) از اهمیت ویژه ای برخوردار است چرا که تعیین اینکه این محاسبات تا چه حد ادامه پیدا کند از اهمیت ویژه ای برخوردار است زیرا هرچه تعداد محاسباتی که برای به دست آوردن دقتی خاص انجام می شود کمتر باشد هزینه ای کمتری ( اعم از زمان و حافظه ) مصرف می شود و تعیین کرانِ پایینِ تعدادِ محاسباتِ لازم به کمک نرخ همگرایی انجام می گیرد.
از جمله کاربردهای دیگر نرخ همگرایی می توان به مسایلی که به «گسسته سازیِ پروسه های پیوسته» می پردازند اشاره کرد.
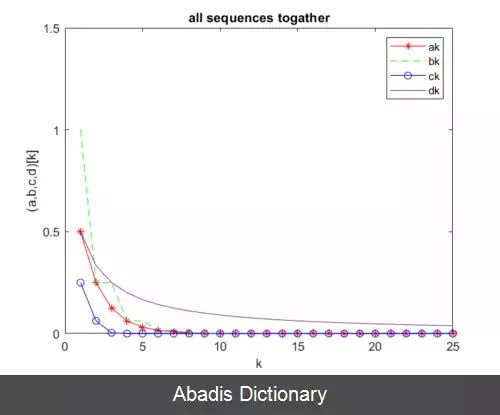
فرض کنید که دنباله دلخواه a k به عدد L همگراست ۱ - می گوییم این دنباله به صورت خطی به عدد L همگراست اگر وجود داشته باشد ضریبی همانند μ ∈ ( 0 , 1 ) به طوری که داشته باشیم:
که در اینصورت به μ نرخ همگرایی می گویند.
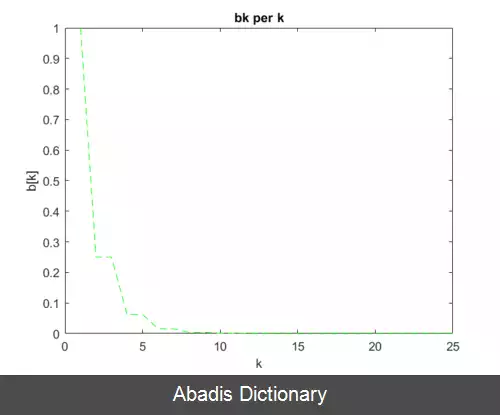
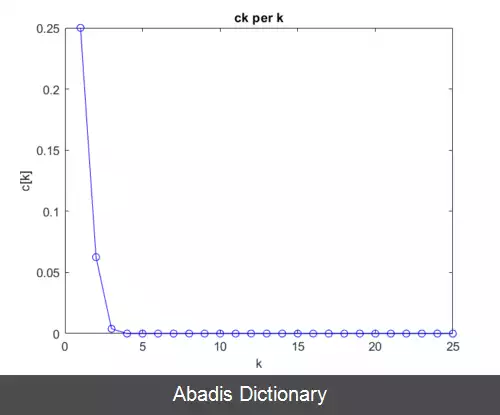
۲ - می گوییم این دنباله به صورت فراخطی ( سریع تر از خطی ) به عدد L همگراست اگر:
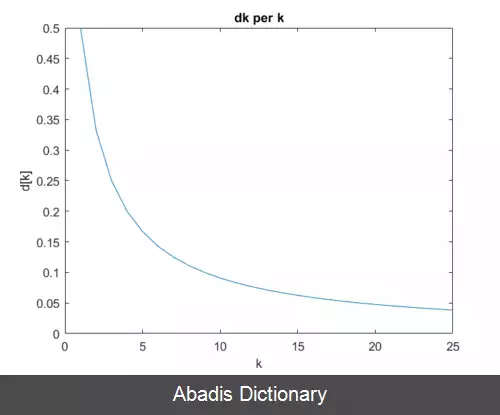
۳ - می گوییم این دنباله به صورت فروخطی ( کندتر از خطی ) به عدد L همگراست اگر: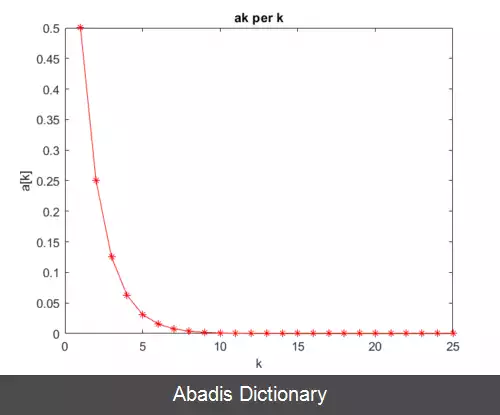

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمفهوم نرخ همگرایی در هنگام کارکردن با برخی دنباله ها از اهمیت ویژه ای برخوردار است، برای مثال دنباله تقریباً اعشاری ( دنبالهٔ تقریبات یک عدد ( مثلاً A ) دنباله ای است که اعضای دنباله رفته رفته به عدد مدنظر ( A ) نزدیک تر می شوند و این نزدیکی عموماً به این صورت است که جمله بعدی نسبت به جمله قبلی یک دهم دقت بیشتر دارد، به عنوان مثال درادامه دنباله تقریبات عدد پی ( π ) آورده شده است: a 1 = 3 , a 2 = 3. 1 , a 3 = 3. 14 , . . . . همان طور که مطرح گردید نرخ همگرایی برای بررسی دنباله تقریباتی که از یک روش تکراری محاسبه ای ( iterative ) همانند گاوس سیدل ( یا هر روش موفق همگرایِ تکراری دیگری ) از اهمیت ویژه ای برخوردار است چرا که تعیین اینکه این محاسبات تا چه حد ادامه پیدا کند از اهمیت ویژه ای برخوردار است زیرا هرچه تعداد محاسباتی که برای به دست آوردن دقتی خاص انجام می شود کمتر باشد هزینه ای کمتری ( اعم از زمان و حافظه ) مصرف می شود و تعیین کرانِ پایینِ تعدادِ محاسباتِ لازم به کمک نرخ همگرایی انجام می گیرد.
از جمله کاربردهای دیگر نرخ همگرایی می توان به مسایلی که به «گسسته سازیِ پروسه های پیوسته» می پردازند اشاره کرد.
فرض کنید که دنباله دلخواه a k به عدد L همگراست ۱ - می گوییم این دنباله به صورت خطی به عدد L همگراست اگر وجود داشته باشد ضریبی همانند μ ∈ ( 0 , 1 ) به طوری که داشته باشیم:
که در اینصورت به μ نرخ همگرایی می گویند.
۲ - می گوییم این دنباله به صورت فراخطی ( سریع تر از خطی ) به عدد L همگراست اگر:
۳ - می گوییم این دنباله به صورت فروخطی ( کندتر از خطی ) به عدد L همگراست اگر:






wiki: نرخ همگرایی
