برای مقایسه دو عدد از نامساوی های تعمیم یافته استفاده می کنیم. برای مثال۱< ۲ به معنای کوچکتر بودن عدد یک دو است. هنگامی که بخواهیم دو بردار را با یکدیگر مقایسه کنیم نیاز به ابزار جدیدی داریم.
در مسائل بهینه سازی و برای مقایسه بردارها و ماتریس ها، به ابزارهای ریاضی قوی تری نیاز داریم. در این حالت نیاز است هنگامی که مقایسه را انجام می دهیم، فضایی مناسب را مطرح کنیم تا مقایسه تحت آن صورت بگیرد. این فضا در مبحث بهینه سازی، مخروط نامیده می شود.
اگر K یک مخروط باشد، تعریف مخروط دوگان به صورت زیر خواهد بود K ∗ = { y | x T y ≥ 0 f o r a l l x ∈ K } به طور شهودی می توان گفت برای تصور کردن دوگان یک مخروط، کافیست خط متعامد بر هر ضلع مخروط اصلی را رسم کنیم. فضای بدست آمده همان مخروط دوگان است.
فرض کنیم مخروط محدب K مناسب[ ۱] باشد. در این حالت می توان گفت مخروط دوگان[ ۲] آن یعنی K ∗ هم مناسب است و می توان نامساوی های تعمیم یافته را با استفاده از آن اجرا کرد. دو ویژگی مهم این نامساوی در زیر آورده شده اند منبع:
1 - y تحت مخروط K ∗ از x بزرگتر است x ≤ K ∗ y اگر و تنها اگر برای هر λ عضو مخروط دوگان K ∗ ، λ ≥ K ∗ 0 داشته باشیم λ T x ≤ λ T y ۲ - تحت مخروط K رابطه x < K y برقرار است اگر و تنها اگر برای هر λ عضو مخروط دوگان K ∗ و مخالف صفر، λ ≥ K ∗ 0 λ ≠ 0 ، داشته باشیم λ T x < λ T y از آنجا که دوگانِ دوگان هر مخروط، خودش است K = K ∗ ∗ لذا روابط بالا در صورتی که جای K و K ∗ هم عوض شود برقرار است. مثلاً λ < K ∗ μ برقرار است اگر و تنها اگر برای هر x ≥ K 0 داشته باشیم λ T x ≤ μ T y [ ۳]
فرض کنید y = T و x = T باشد. مخروط دوگان نیز K ∗ = R + یا ربع مثبت صفحه است. اگر λ = باشد واضح است که تحت این مخروط y ≥ x است چراکه T = 1 + 2 = 3 ≤ T = 3 + 4 = 7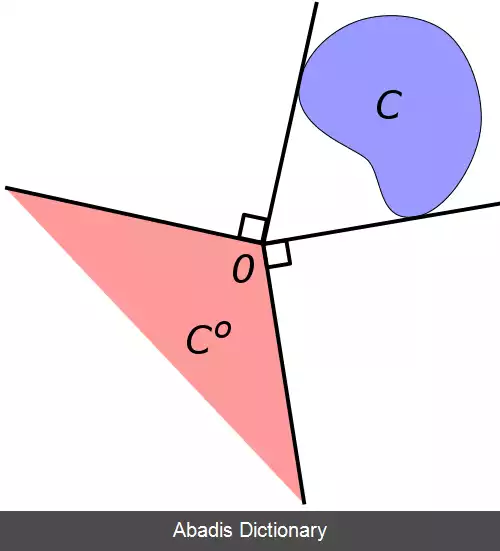
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر مسائل بهینه سازی و برای مقایسه بردارها و ماتریس ها، به ابزارهای ریاضی قوی تری نیاز داریم. در این حالت نیاز است هنگامی که مقایسه را انجام می دهیم، فضایی مناسب را مطرح کنیم تا مقایسه تحت آن صورت بگیرد. این فضا در مبحث بهینه سازی، مخروط نامیده می شود.
اگر K یک مخروط باشد، تعریف مخروط دوگان به صورت زیر خواهد بود K ∗ = { y | x T y ≥ 0 f o r a l l x ∈ K } به طور شهودی می توان گفت برای تصور کردن دوگان یک مخروط، کافیست خط متعامد بر هر ضلع مخروط اصلی را رسم کنیم. فضای بدست آمده همان مخروط دوگان است.
فرض کنیم مخروط محدب K مناسب[ ۱] باشد. در این حالت می توان گفت مخروط دوگان[ ۲] آن یعنی K ∗ هم مناسب است و می توان نامساوی های تعمیم یافته را با استفاده از آن اجرا کرد. دو ویژگی مهم این نامساوی در زیر آورده شده اند منبع:
1 - y تحت مخروط K ∗ از x بزرگتر است x ≤ K ∗ y اگر و تنها اگر برای هر λ عضو مخروط دوگان K ∗ ، λ ≥ K ∗ 0 داشته باشیم λ T x ≤ λ T y ۲ - تحت مخروط K رابطه x < K y برقرار است اگر و تنها اگر برای هر λ عضو مخروط دوگان K ∗ و مخالف صفر، λ ≥ K ∗ 0 λ ≠ 0 ، داشته باشیم λ T x < λ T y از آنجا که دوگانِ دوگان هر مخروط، خودش است K = K ∗ ∗ لذا روابط بالا در صورتی که جای K و K ∗ هم عوض شود برقرار است. مثلاً λ < K ∗ μ برقرار است اگر و تنها اگر برای هر x ≥ K 0 داشته باشیم λ T x ≤ μ T y [ ۳]
فرض کنید y = T و x = T باشد. مخروط دوگان نیز K ∗ = R + یا ربع مثبت صفحه است. اگر λ = باشد واضح است که تحت این مخروط y ≥ x است چراکه T = 1 + 2 = 3 ≤ T = 3 + 4 = 7

wiki: نامساوی های تعمیم یافته
